Linked list
연결 리스트는 노드라는 단위로 구성되며 각 노드는 데이터와 다음 노드를 가리키는 포인터를 가지고 있다.
동적으로 메모리를 할당받아서 사용하기 때문에 element 추가 및 삭제가 쉽다.
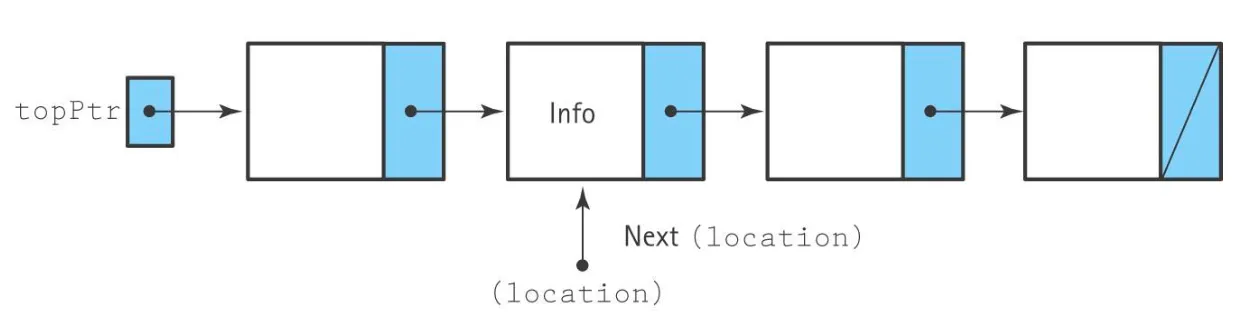
topPtr는 head라고도 하며 연결 리스트의 시작점을 가리킨다. 리스트가 비어있다면 헤드는 nullptr를 가리킨다.
동적 메모리 할당으로 삽입 및 삭제가 빠르지만 포인터 저장을 위한 추가 메모리가 필요하다.
Struct NodeType {
ItemType info;
NodeType *next;
};
C++
복사
Stack Implementation
array를 사용하지 않고 dynamic allocation을 사용해서 stack에 element를 push하도록 내부 구현을 변경할 수 있다. Push, Pop, IsEmpty등 외부적으로는 동일하지만 내부에서는 linked list를 활용해서 구현한다.
new연산자는 heap에다 공간을 할당한 다음 그 위치를 가리키는 포인터를 리턴한다.
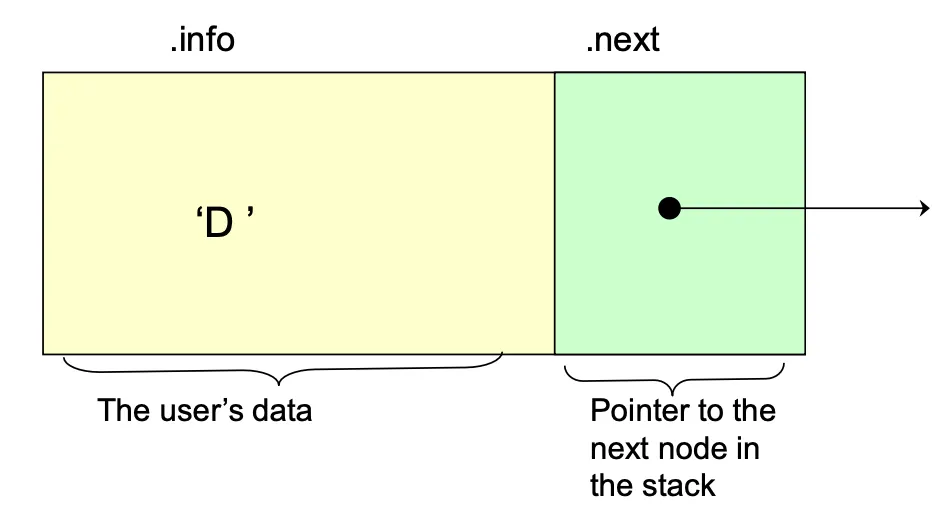
linked list는 node를 이어서 만든 list이다. 각 노드는 info와 next로 구성되어있다.
info에는 user가 넣을 데이터가 들어가고 next는 다음 노드의 위치를 가리키는 포인터가 들어간다.
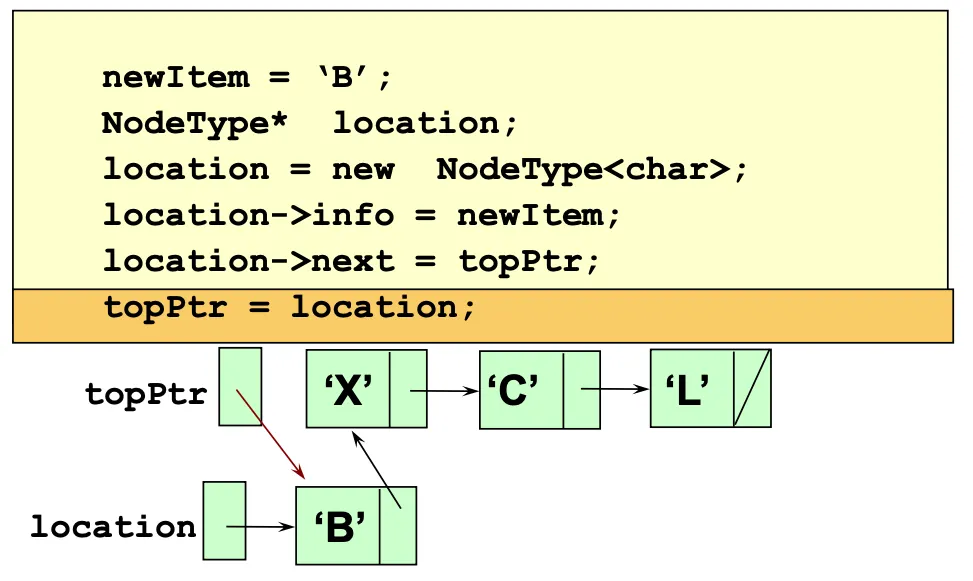
Implementing Push
void StackType::Push(ItemType newItem)
// Adds newItem to the top of the stack.
{
if (IsFull())
throw FullStack();
NodeType *location;
location = new NodeType<ItemType>;
location->info = newItem;
location->next = topPtr;
topPtr = location;
}
C++
복사
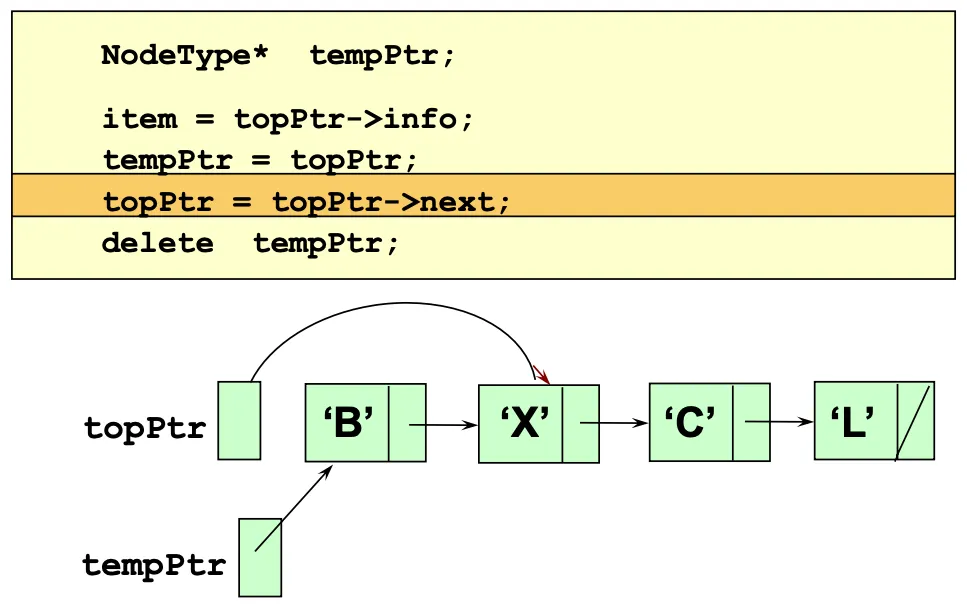
Implementing Pop
void StackType::Pop() // Remove top item from Stack.
{
if (IsEmpty())
throw EmptyStack();
else {
NodeType *tempPtr;
tempPtr = topPtr;
topPtr = topPtr->next;
delete tempPtr;
}
}
ItemType StackType::Top()
// Returns a copy of the top item in the stack.
{
if (IsEmpty())
throw EmptyStack();
else
return topPtr->info;
39
}
C++
복사
array가 아니니까 index를 사용할 필요가 없다.
destructor
delete topPtr; 한다고 해서 topPtr이 가리키고 있는 모든 노드들이 해제되지는 않는다. while문을 통해서 순회하면서 하나씩 해제해줘야한다.
stackType::~StackType()
// Post: stack is empty;
// All items have been deallocated.
{
NodeType *tempPtr;
while (topPtr != NULL) {
tempPtr = topPtr;
topPtr = topPtr->next;
delete tempPtr;
}
}
C++
복사
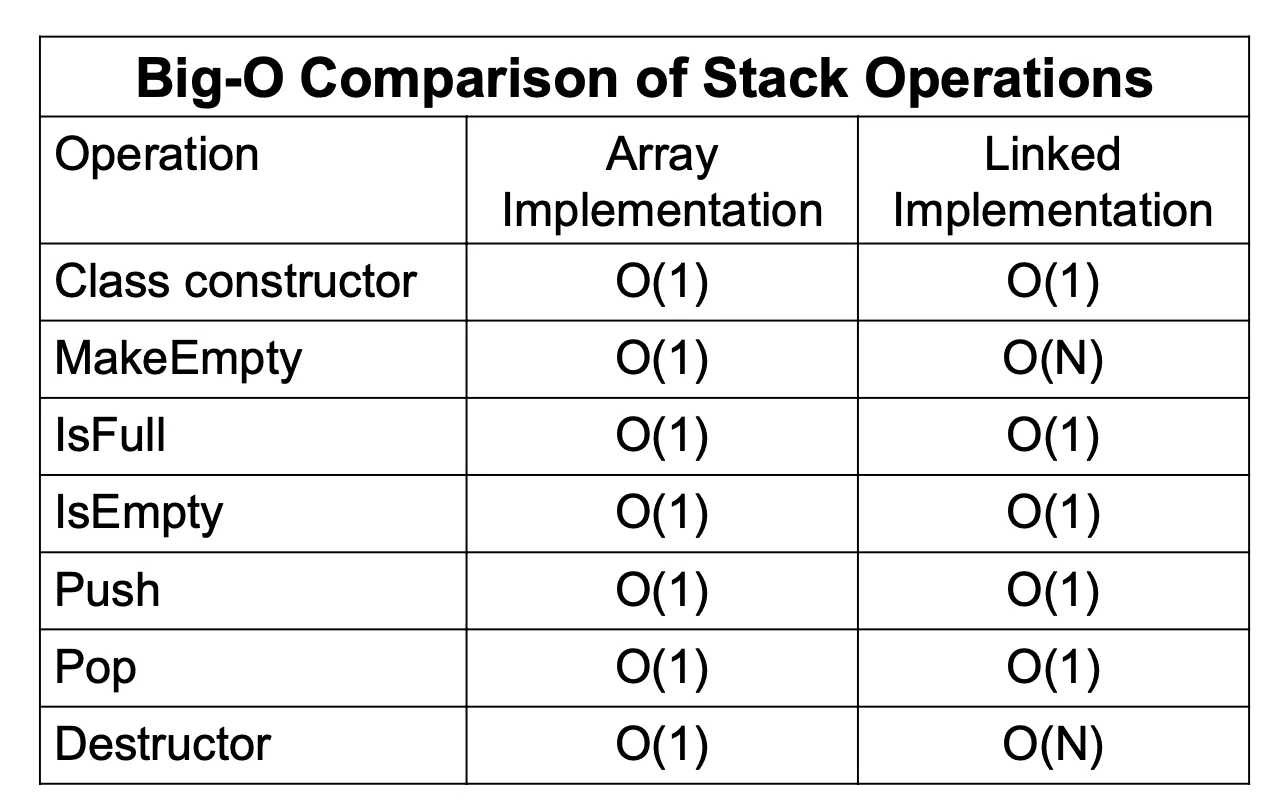
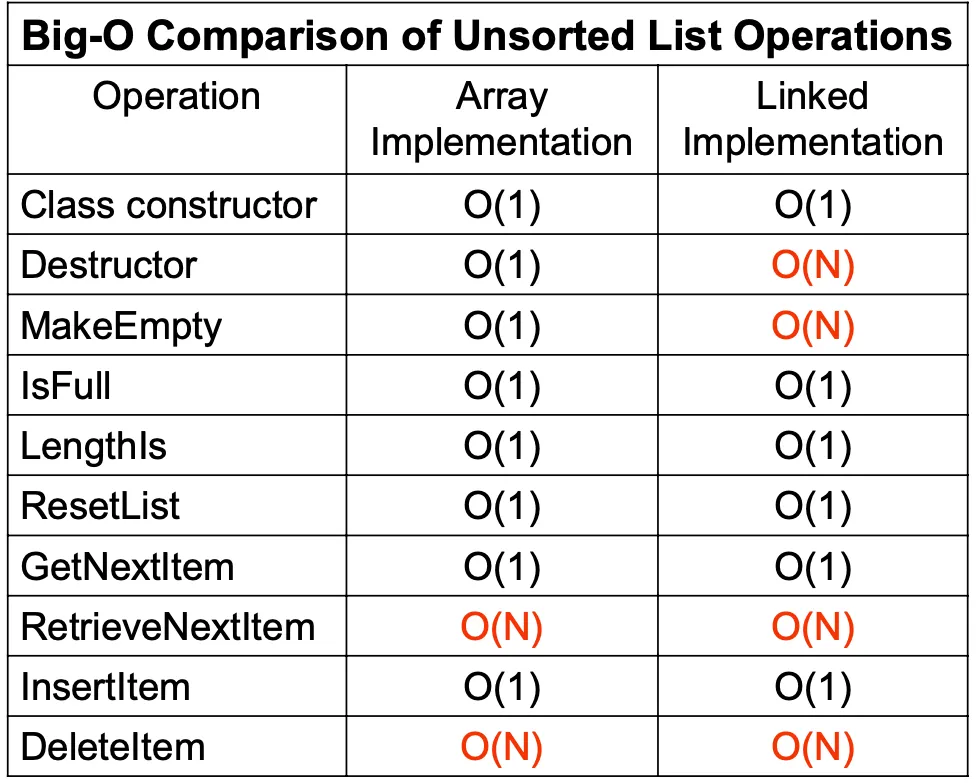
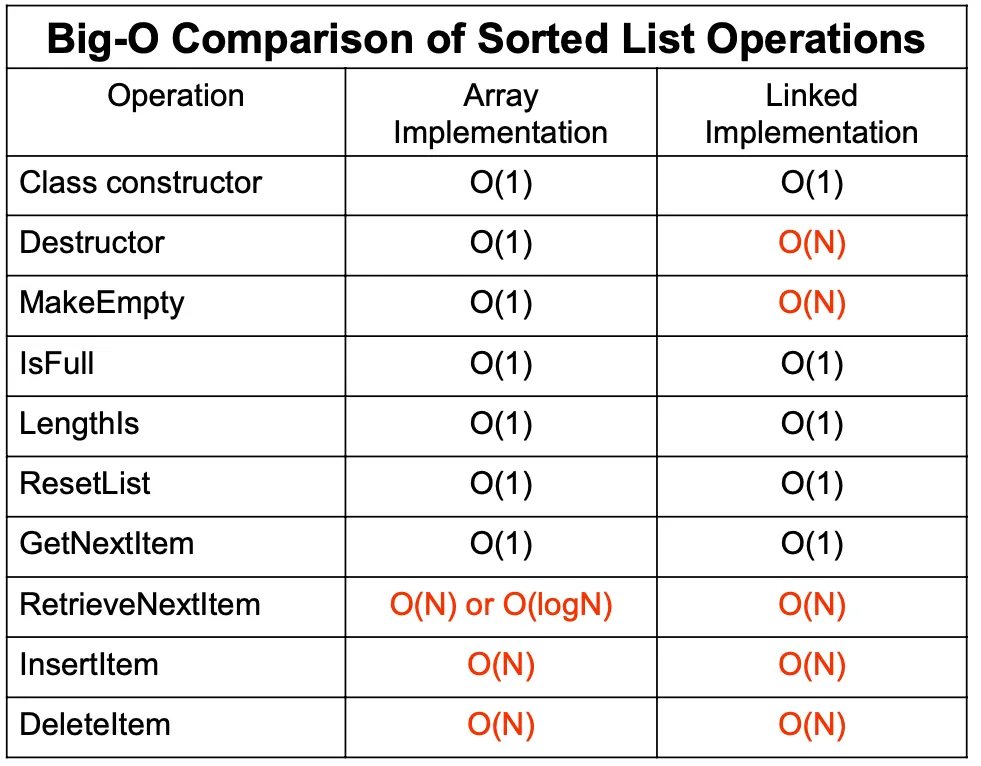
Comparing Stack implementations
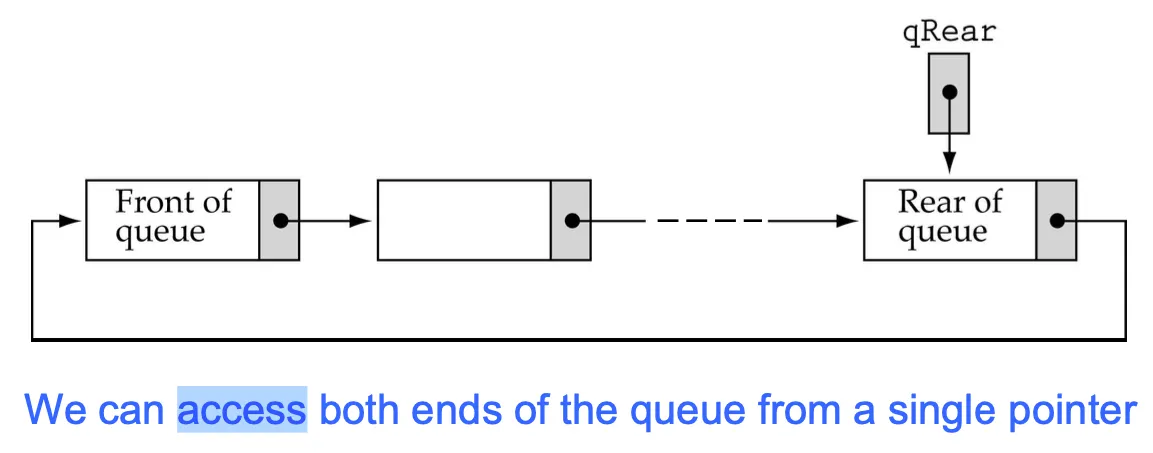
Queue implementation
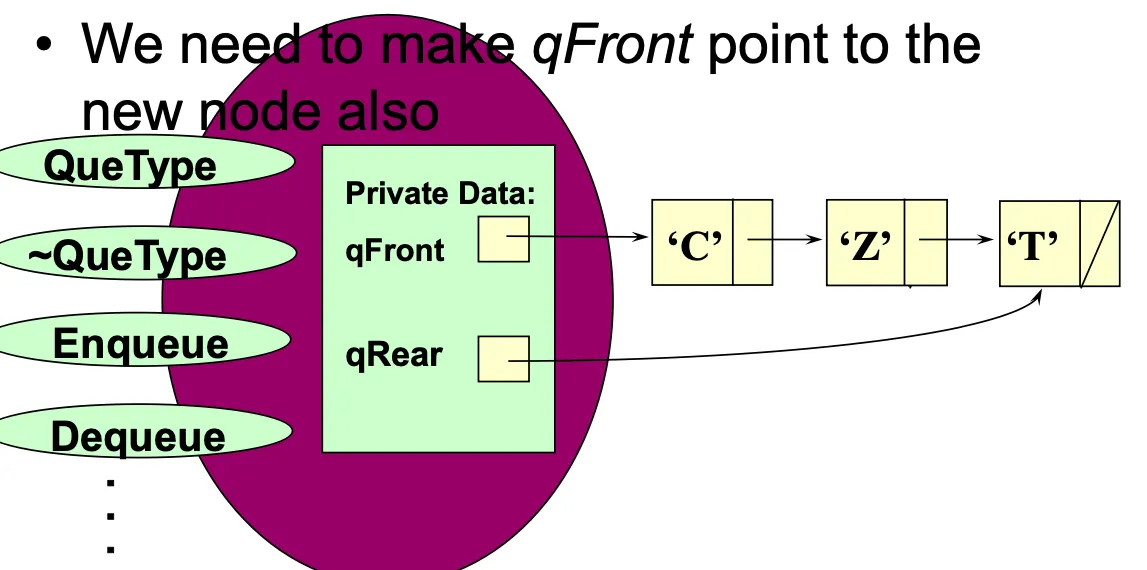
empty queue에 enqueuing하는경우 qFront도 새로 생긴 노드를 가리켜야함.
item이 한개 남은 queue에 dequeuing하는 경우 qFront와 qRear 둘다 NULL을 가리켜야 함.
#include "ItemType.h" // for ItemType
template <class ItemType> class QueType {
public:
QueType(); // CONSTRUCTOR
~QueType(); // DESTRUCTOR
bool IsEmpty() const;
bool IsFull() const;
void Enqueue(ItemType item);
void Dequeue(ItemType &item);
void MakeEmpty();
private:
NodeType<ItemType> *qFront;
NodeType<ItemType> *qRear;
};
template <class ItemType>
QueType<ItemType>::QueType() // CONSTRUCTOR
{
qFront = NULL;
qRear = NULL;
}
template <class ItemType> bool QueType<ItemType>::IsEmpty() const {
return (qFront == NULL)
}
template <class ItemType>
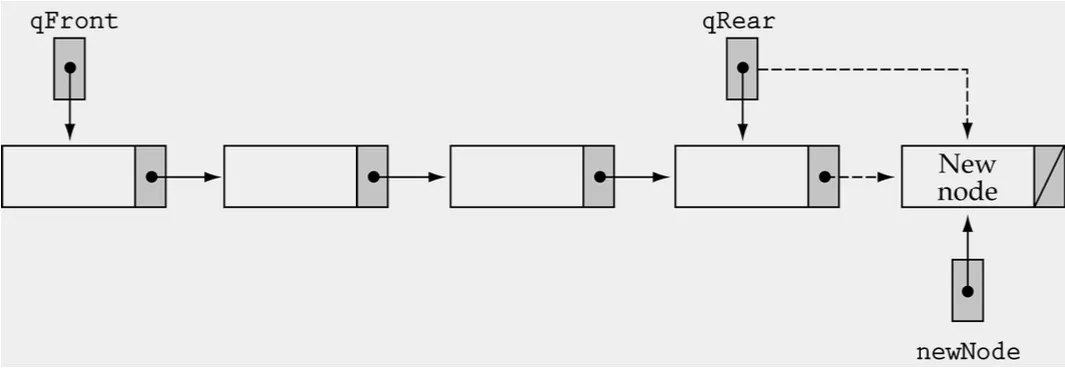
void QueType<ItemType>::Enqueue(ItemType newItem)
// Adds newItem to the rear of the queue.
// Pre: Queue has been initialized.
// Queue is not full.
// Post: newItem is at rear of queue.
{
NodeType<ItemType> *ptr;
ptr = new NodeType<ItemType>;
ptr->info = newItem;
ptr->next = NULL;
if (qRear == NULL)
qFront = ptr;
else
qRear->next = ptr;
qRear = ptr;
}
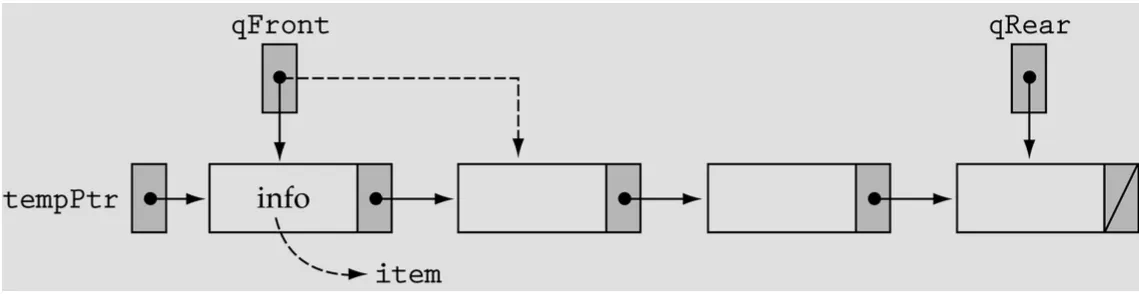
template <class ItemType>
void QueType<ItemType>::Dequeue(ItemType &item)
// Removes element from from front of queue
// and returns it in item.
// Pre: Queue has been initialized.
// Queue is not empty.
// Post: Front element has been removed from queue.
// item is a copy of removed element.
{
NodeType<ItemType> *tempPtr;
tempPtr = qFront;
item = qFront->info;
qFront = qFornt->next;
if (qFront == NULL)
qRear = NULL;
delete tempPtr;
}
C++
복사
Circular linked Queue
Memory Requirements
•
Array-based implementation
• Assume a queue (size: 100) of strings (80bytes each)
• Assume indices take 2 bytes
• Total memory: (80 bytes x 101 slots) + (2bytes x 2 indexes) = 8084 bytes
•
Linked-list-based implementation
• Assume pointers take 4 bytes
• Total memory per node: 80 bytes + 4 bytes = 84 bytes
linked list를 사용하는 경우 elements의 개수가 적으면 메모리를 적게 차지하지만
linked list를 사용한다고 항상 메모리를 적게 쓰는것은 아님.
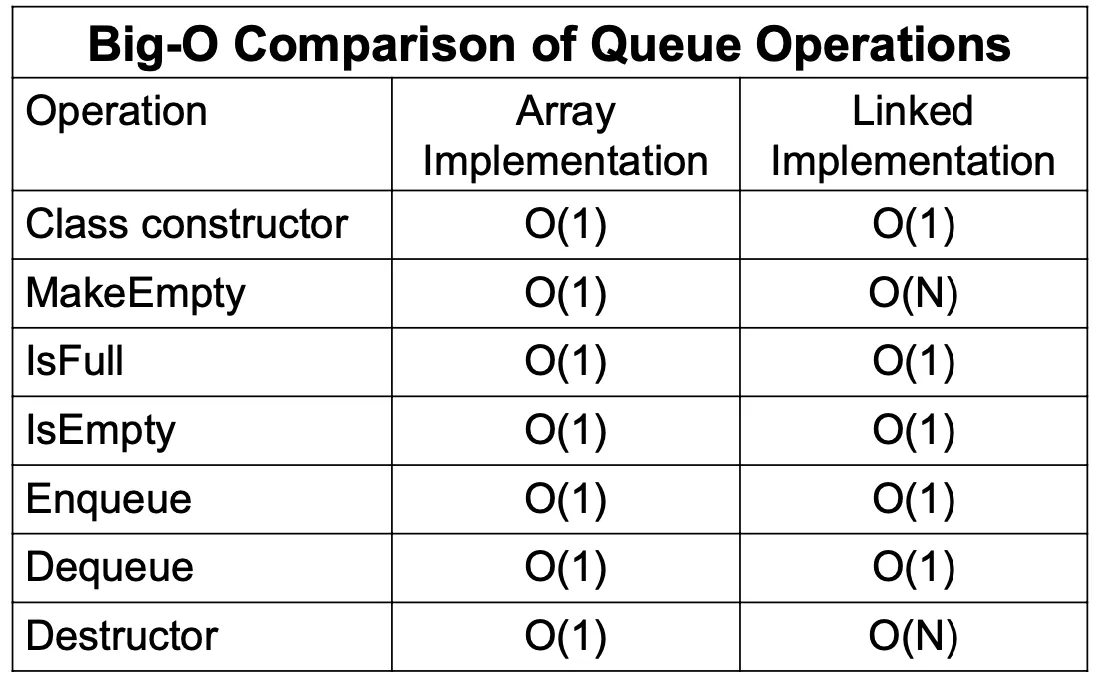
Comparing Queue implementations
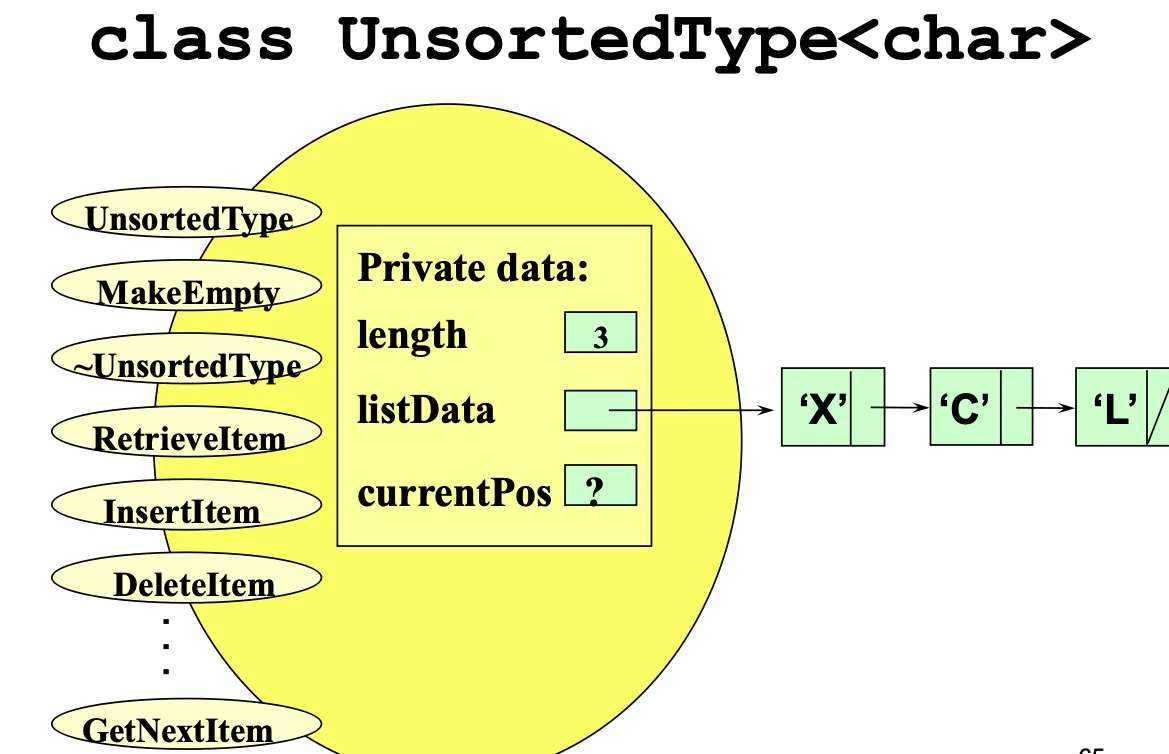
Linked Unsorted List
#include “itemtype.h”
template <class ItemType>
UnsortedType<ItemType>::UnsortedType() // constructor
// Pre: None.
// Post: List is empty.
{
length = 0;
listData = NULL;
}
template <class ItemType>
int UnsortedType<ItemType>::LengthIs() const
// Post: Function value = number of items in the list.
{
return length;
}
template <class ItemType>
void UnsortedType<ItemType>::RetrieveItem(ItemType &item, bool &found)
// Pre: Key member of item is initialized.
// Post: If found, item’s key matches an element’s key in the list
// and a copy of that element has been stored in item; otherwise,
// item is unchanged.
{
bool moreToSearch;
NodeType<ItemType> *location;
location = listData;
found = false;
moreToSearch = (location != NULL);
while (moreToSearch && !found) {
if (item == location->info) // match here
{
found = true;
item = location->info;
} else // advance pointer
{
location = location->next;
moreToSearch = (location != NULL);
}
}
}
C++
복사
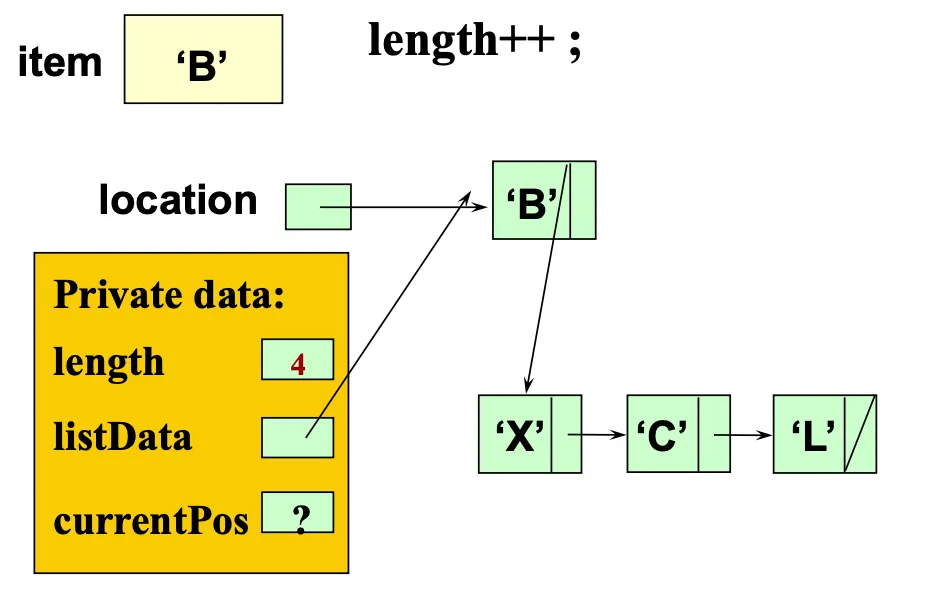
InsertItem implementation
template <class ItemType>
void UnsortedType<ItemType>::InsertItem(ItemType item)
// Pre: list is not full and item is not in list.
// Post: item is in the list; length has been incremented.
{
NodeType<ItemType> *location;
// obtain and fill a node
location = new NodeType<ItemType>;
location->info = item;
location->next = listData;
listData = location;
length++;
}
C++
복사
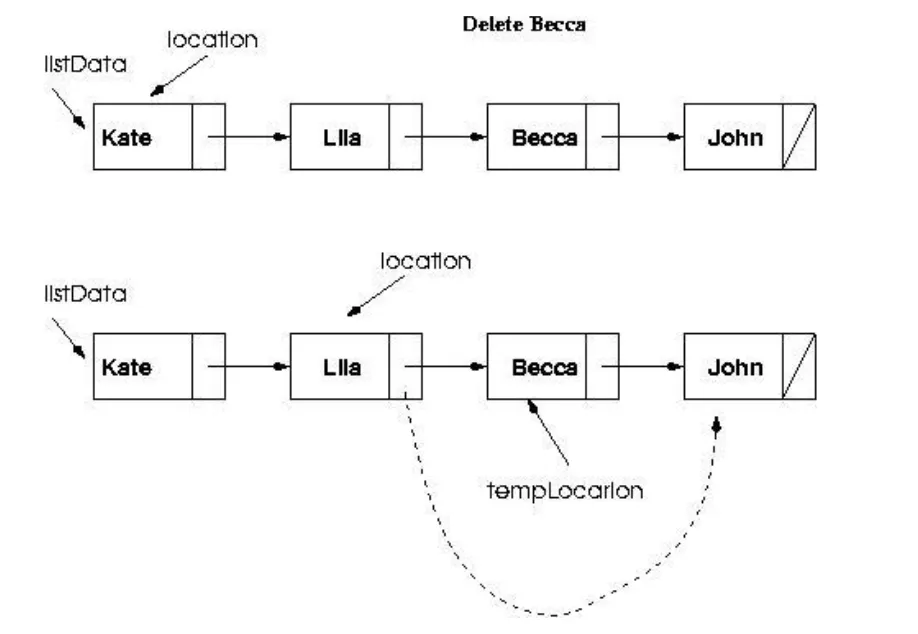
DeleteItem implementation
item을 먼저 찾고, 삭제할 노드의 previous node의 포인터를 변경해야한다. 다음 노드로 넘어가면 previous node의 주소를 알수없는데 어떻게?
(location→next)→info로 접근해서 item을 찾는다. 앞선 칸에서 다음 칸에 찾는 item이 있는지 확인하는 것이다. 첫번째 칸을 지워야 하는 경우는 예외처리해준다.
이 구현은 삭제할 아이템이 list안에 있을 경우에만 동작한다.
template <class ItemType>
void UnsortedType<ItemType>::DeleteItem(ItemType item) {
NodeType<ItemType> *location = listData;
NodeType<ItemType> *tempLocation;
if (item == listData->info) {
tempLocation = location;
listData = listData->next; // delete first node
} else {
while (!(item == (location->next)->info))
location = location->next;
// delete node at location->next
tempLocation = location->next;
location->next = (location->next)->next;
}
delete tempLocation;
length--;
}
C++
복사
Sorted List implementation
RetriveItem
template <class ItemType>
void SortedType<ItemType>::RetrieveItem(ItemType &item, bool &found) {
NodeType<ItemType> *location;
location = listData;
found = false;
while ((location != NULL) && !found) {
if (location->info < item)
location = location->next;
else if (location->info == item) {
found = true;
item = location->info;
} else
location = NULL; // no reason to continue
}
}
C++
복사
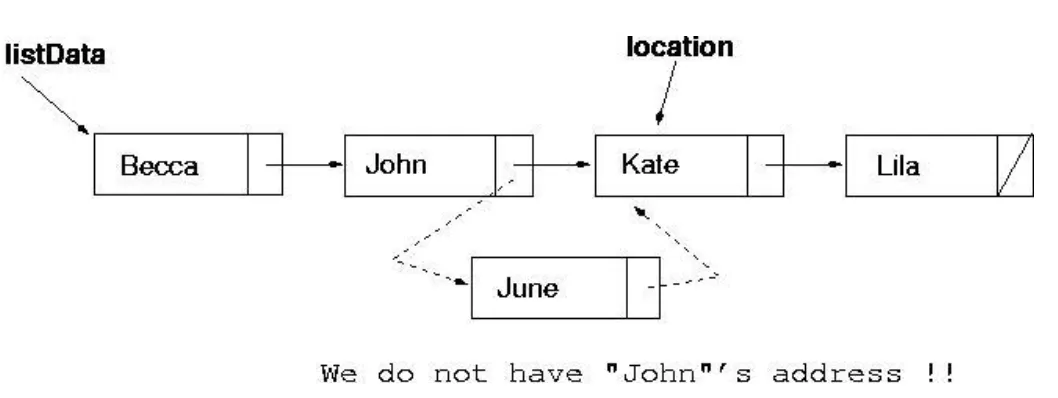
InsertItem
Kate 앞에 들어가야한다는 것을 알게 됐을 때, John의 next가 June을 가리켜야 한다. 하지만 John의 address가 없으므로 변경할 수 없다. location이 가리키고 있지 않기 때문.
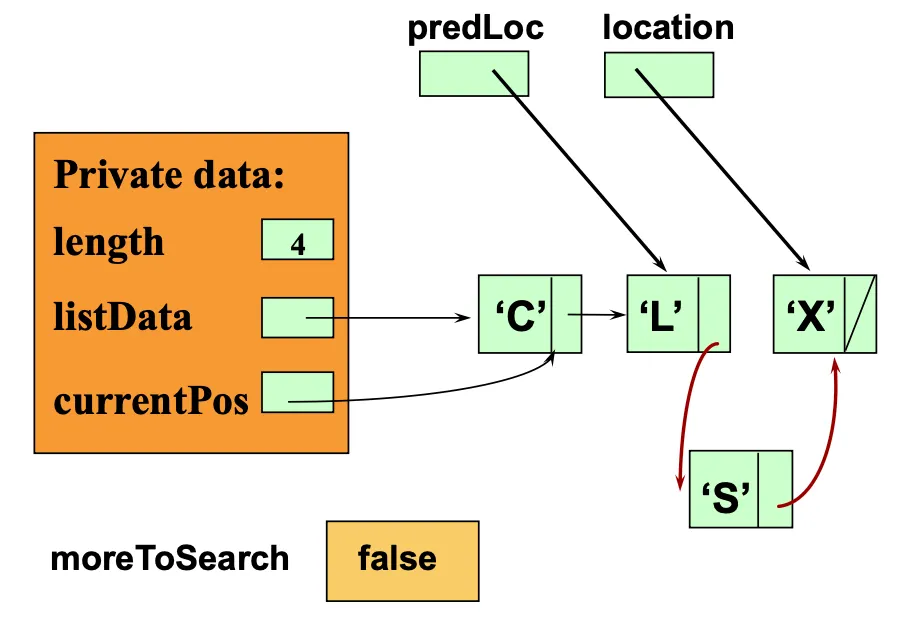
solution: predLoc과 location의 두 개의 포인터를 사용해서 새 element를 삽입할 위치를 찾는다.
predLoc이 앞에 있고 location이 뒤에 있다.
location이 첫번째 요소를 가리키고 predLoc은 NULL로 초기화한다.
location이 두번째 요소를 가리키면 predLoc은 이전 요소를 가리킨다.
한칸씩 진행하다가 moreToSearch가 false가 되면
predLoc으로 이전 노드의 next에 접근해서 newNode를 가리키도록 변경하고 newNode의 next는 location을 가리키도록 설정한다.
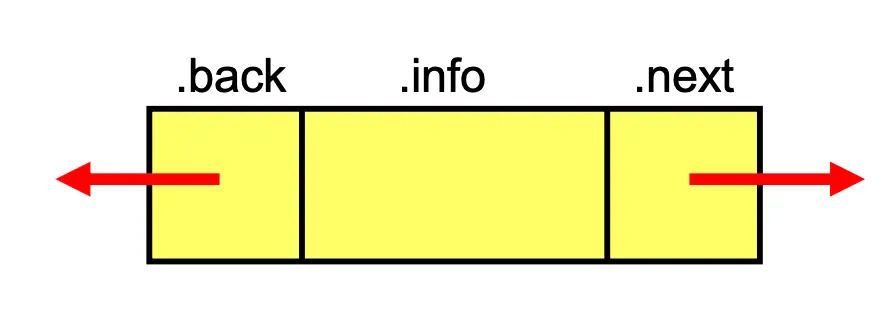
Doubly linked list
A doubly linked list is a list in which each node is linked to both its successor and its predecessor.
info: the user’s data
next, back: address of the next and previous node in the list
Sorted list는 중간에 끼어드는 경우에 문제가 있어서 doubly linked list로 해결한다. unsorted인 경우 필요없다.
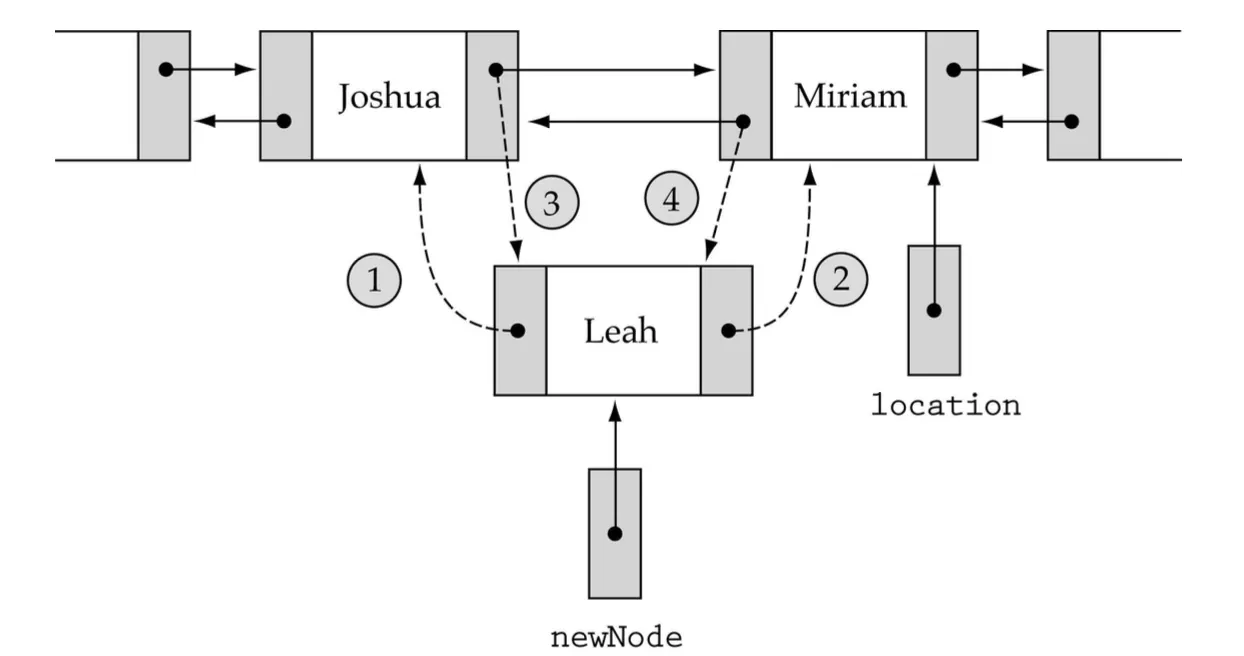
1.
newNode->back = location->back;
2.
newNode->next = location
3.
location->back->next=newNode;
4.
location->back = newNode;