Arithmetics

곱셈, 나눗셈 등은 어떻게 수행되고 분수, 실수를 어떻게 표현할 것인가.

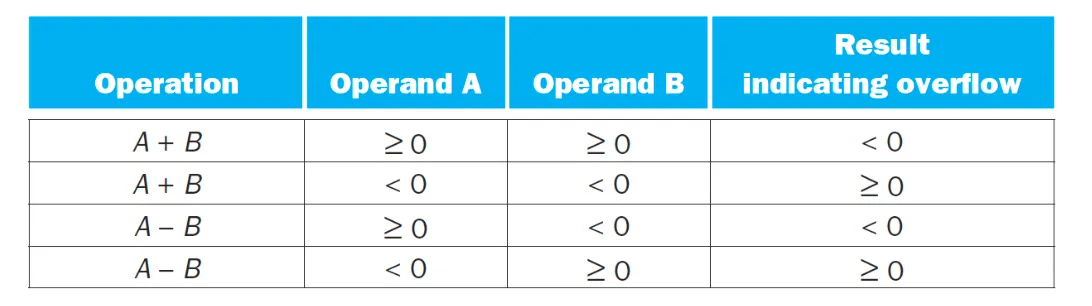
Overflow

overflow는 값이 표현할 수 있는 범위를 벗어날때 발생하고 underflow표현할수있는 값보다 작아질 때 발생함.

다른 부호의 값들을 더할때는 overflow가 발생할 수 없다.

양수랑 양수를 더했는데 최상위비트가 1이면 음수가 되고 overflow가 발생했음을 알 수 있다.

반대로 negative숫자를 더했는데 sign bit가 0이 나와도 overflow가 일어났다.

unsigned instruction은 오버플로우가 일어나도 exception발생시키지 않는다.

C언어는 overflow를 무시한다. Signed instruction은 overflow에 exception을 발생시킨다.

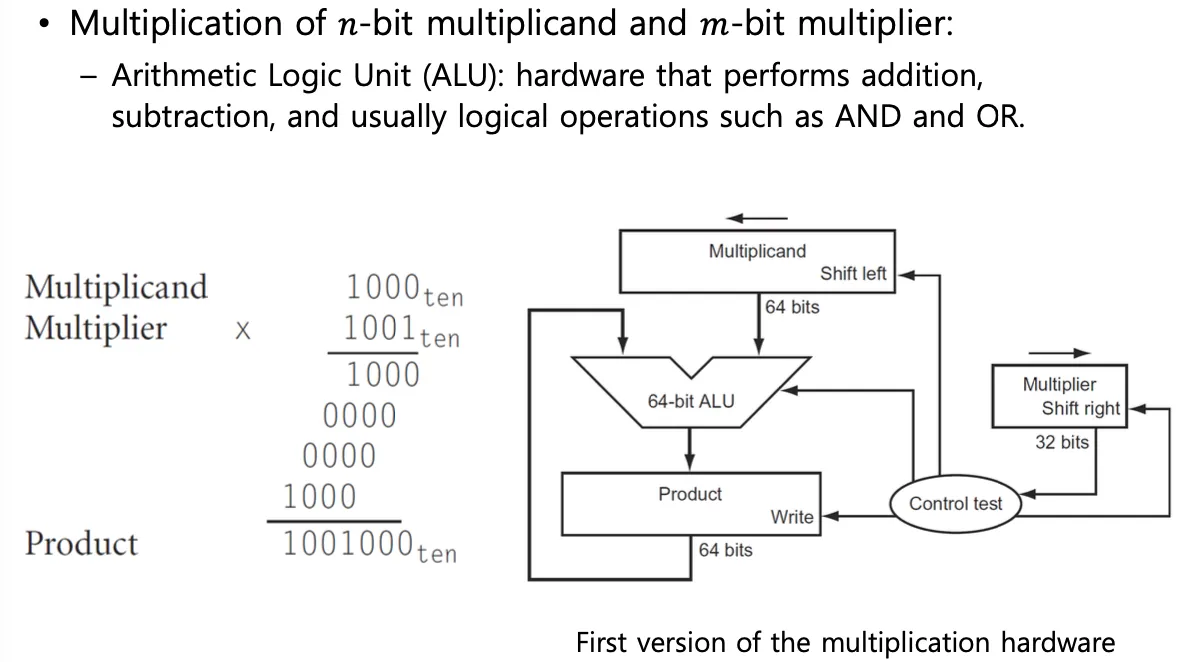
Multiplication

multiplier = 곱할 수. multiplicand = 곱해지는 수

ALU = arithmetic logic unit 산수, 논리연산을 수행하는 하드웨어 유닛. ex) add, and, or

multiplicand는 64비트로 오른쪽부터 채워나간다.

datapath는 명령에 따라서 계산되는 정해진 흐름으로 레지스터, ALU등을 포함한다. control test는 제어신호를 생성해서 datapath에서의 연산을 조정한다.

product은 곱한 결과를 저장하는 하드웨어로 0으로 초기화되어있음.

multiplier와 multiplicand의 곱셈 결과가 길어질 수 있기 때문에 64비트이다.

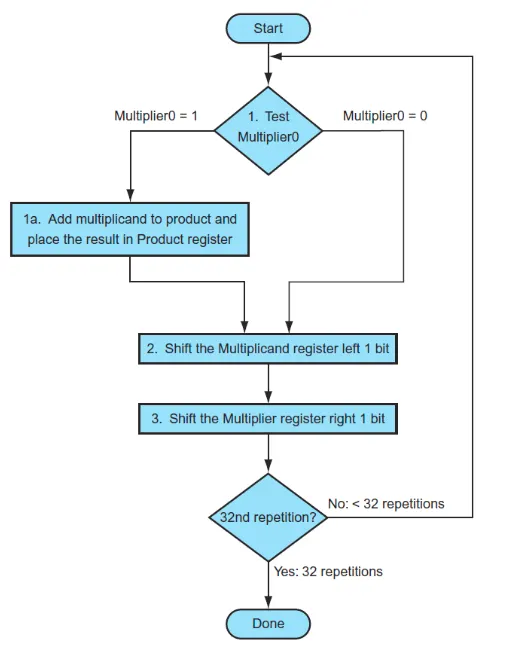
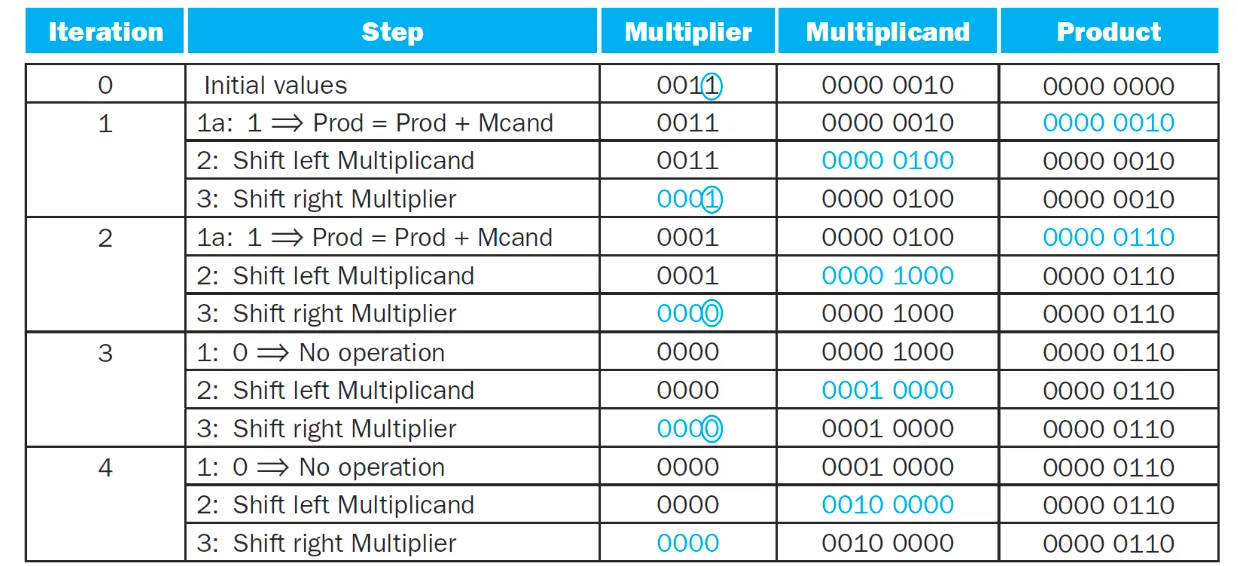
처음에는 multiplier의 0번째 비트를 control test로 보내서 0인지 1인지 확인하고 1인 경우 product에 multiplicand더하고 결과를 product에 저장한다. add명령은 ALU가 수행한다.

product은 결과를 받아서 control test의 명령에 의해 1을 주면 쓰고 0을 주면 아무것도 안한다.

이후 왼쪽으로 multiplicand를 shift한다 multiplier는 오른쪽으로 shift한다. 비트 하나를 지우는것과 같다. 하나씩 지워나가며 32번 반복한다. 만약에 16비트라면 16번 반복한다.

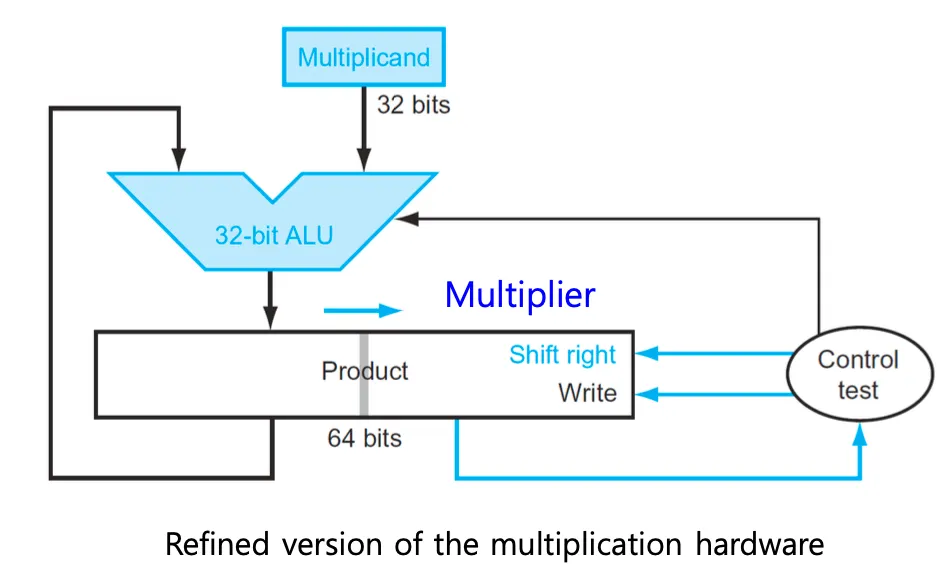
Refined version

속도를 올리고싶으면 operation을 병렬로 처리하면된다.

32bit ALU는입력과 출력이 반드시 32비트를 가진다. 64비트면 입력과 출력이 64비트이다.

multiplier는 product의 오른쪽에 들어가고 product가 ALU에 32비트만 입력으로 준다.

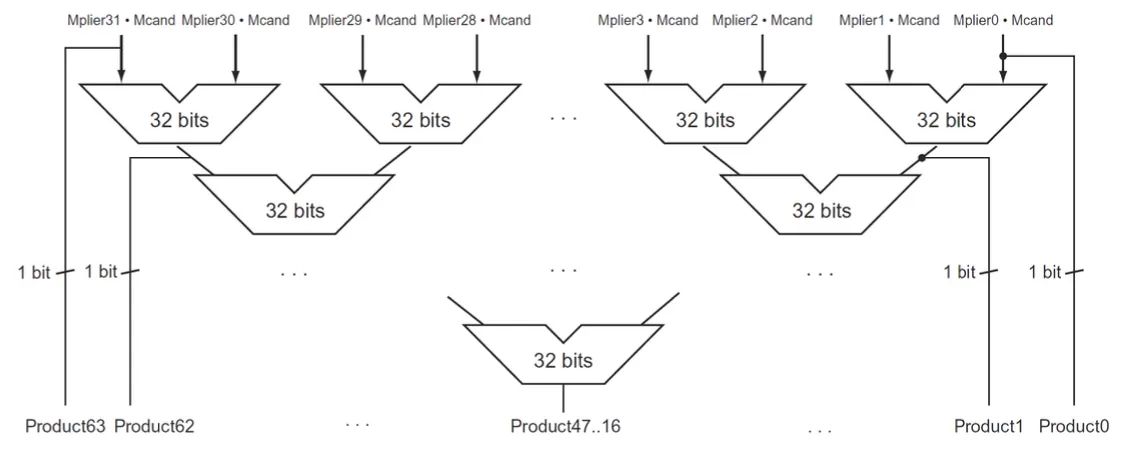
ALU를 여러개 쌓아서 병렬적으로 계산하면 빠르게 계산할 수 있다.

4비트를 계산하면 4개의 ALU가 필요하다.

signed multiplication을 계산할 때는 부호를 없애고 곱한 값에 나중에 부호를 붙인다.

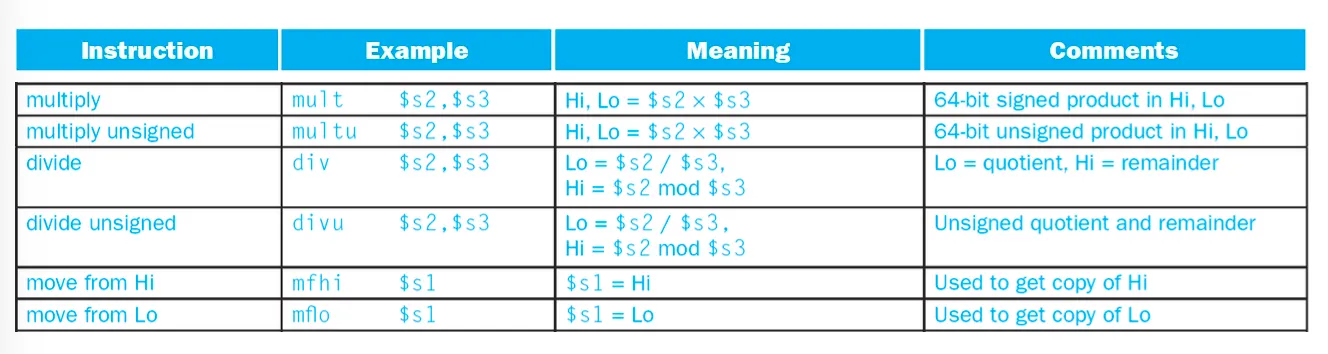
Multiply In MIPS

product를 저장하기 위해서 32비트짜리 레지스터 2개를 할당함: Hi, Lo

mult rs rt나 multu rs rt를 사용함.

rs가 3 rt가 2라면 각각을hi Lo에 나눠서 넣는다

mfhi rd = move from Hi, mflo rd = move from Lo

Hi를 rd로 복사, Lo를 rd로 복사

Hi Lo는 gpr이 아니라서 건드릴수 있는 값이 아니다

mult rd rs rt를 쓰면 rs,rt의 곱셈값이 Hi, Lo에 저장되기때문에 하위 32비트를 가져오려면 원래는

mult rs, rt

mflo rd를 수행해야한다. 실제로 어셈블러는 mul rd rs rt를 이렇게 해석한다.

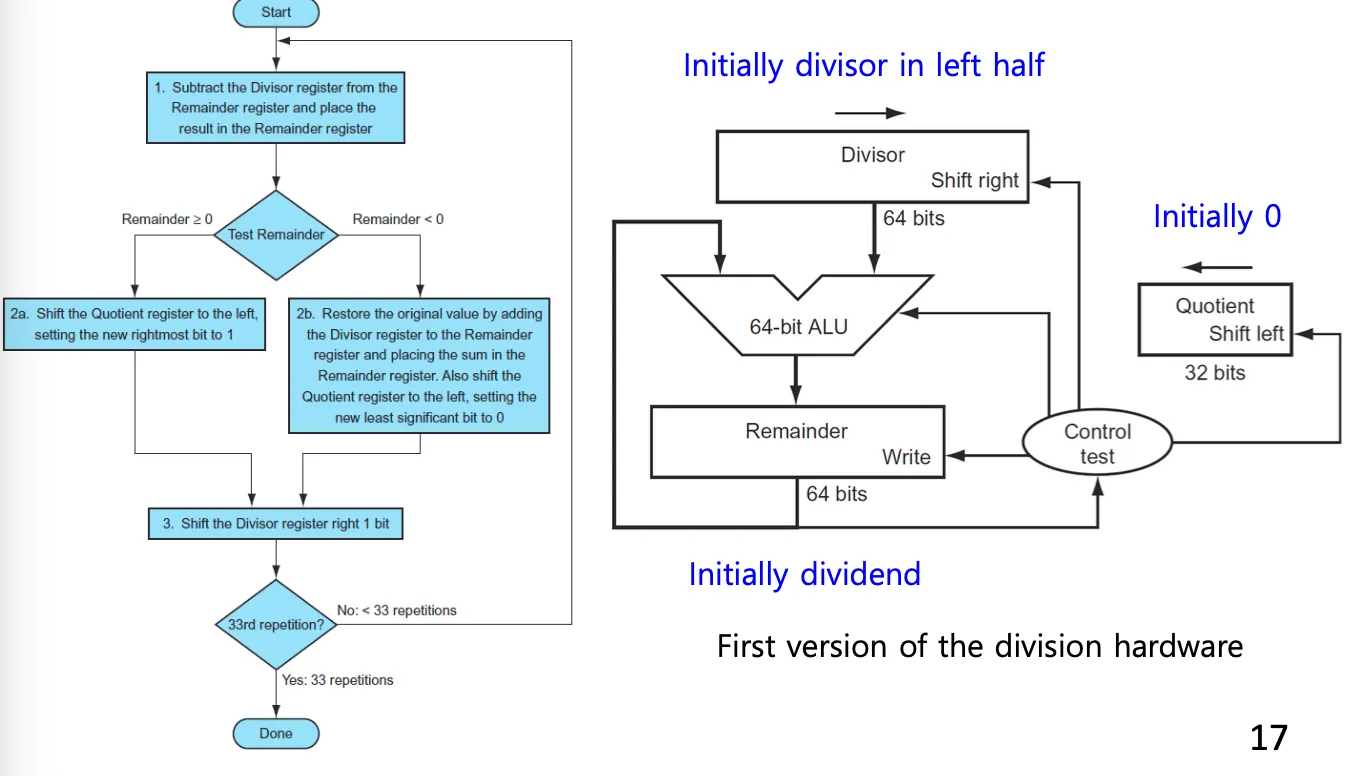
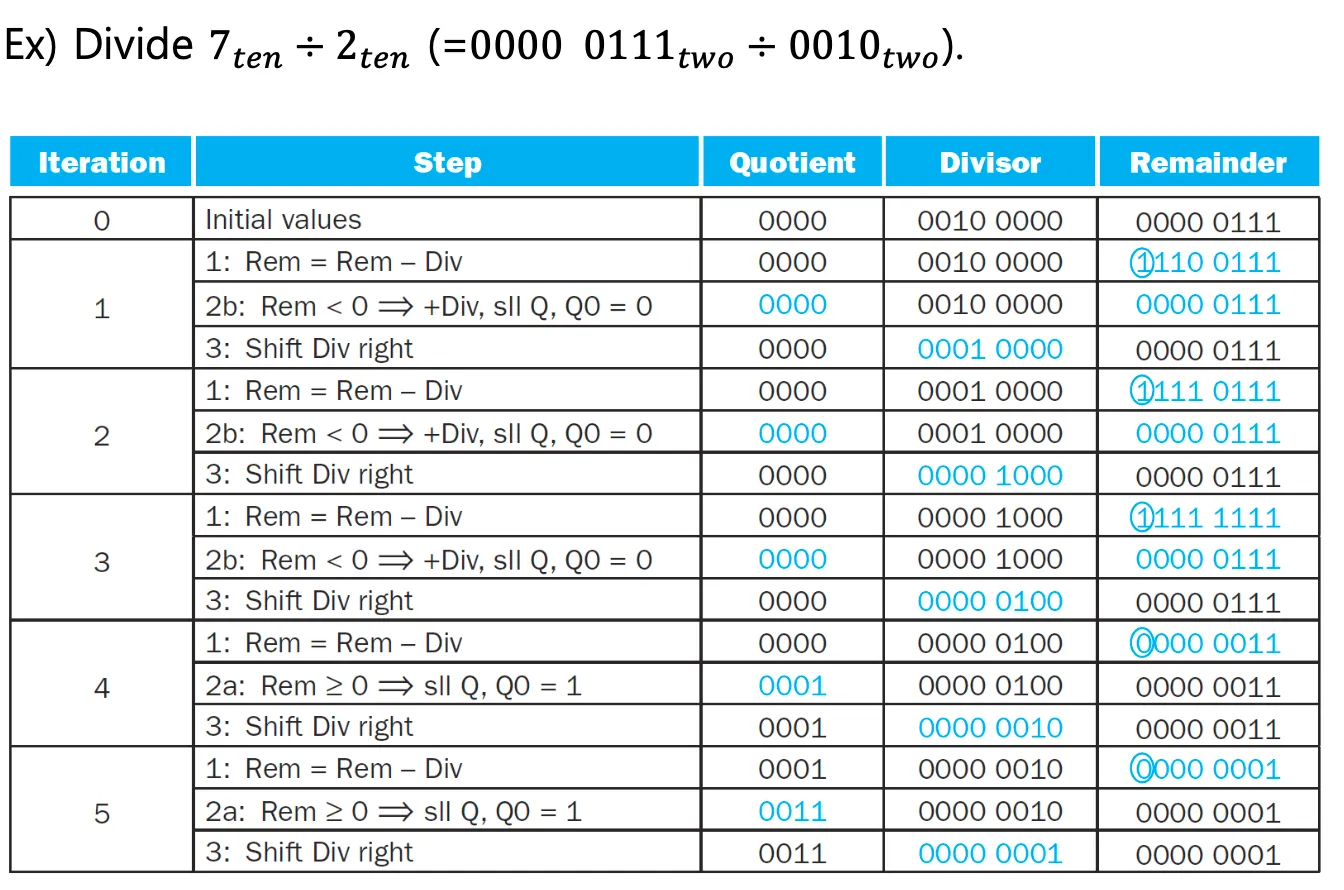
Division

dividend = 나뉘는 수 divisor = 나누는 수

dividend = quotient * divisor + remainder

컴퓨터는 1000과 1중 뭐가 더 큰지 알려면 빼보고 1000에서 1빼서 양수이면 1000이 크다고 알 수 있다.

따라서 비교를 위해서 빼는 연산을 먼저 해보고 restore해준다.

remainder, divisor 64비트를 가져와서 remainder에서 divisor를 빼고 결과를 remainder에 저장한다.

control test가 remainder가 0이상인지 미만인지 계산해서 0이상이면 quotient register를 sll하고 오른쪽에 생긴 한 칸은 1로 채운다.

0미만이면 remainder에 divisor를 더해서 remainder를 복구시켜주고 quotient register를 sll하고 오른쪽에 생긴 한 칸은 0으로 채운다.

divisor register에 srl을 수행한다

33번째 operation이면 끝내고 아니면 반복한다.

33번 수행하는 이유는 첫번째 iteration은 무조건 음수가 나오기 때문에 의미가 없어서이다.

refined버전에서는 처음에 한번 shift해놓고 시작한다.

divison은 뺄셈 부호를 알아야하기 때문에 parallel을 사용할수없다. SRT division이라는 방식을 사용함.

Division in MIPS

결과를 Hi, Lo에 저장한다. div rs,rt / divu rs, rt

Hi에는 remainder가 저장되고 Lo에는 Quotient가 저장된다.

mfhi mflo사용해서 rd로 카피해옴 gpr로

Floating Point

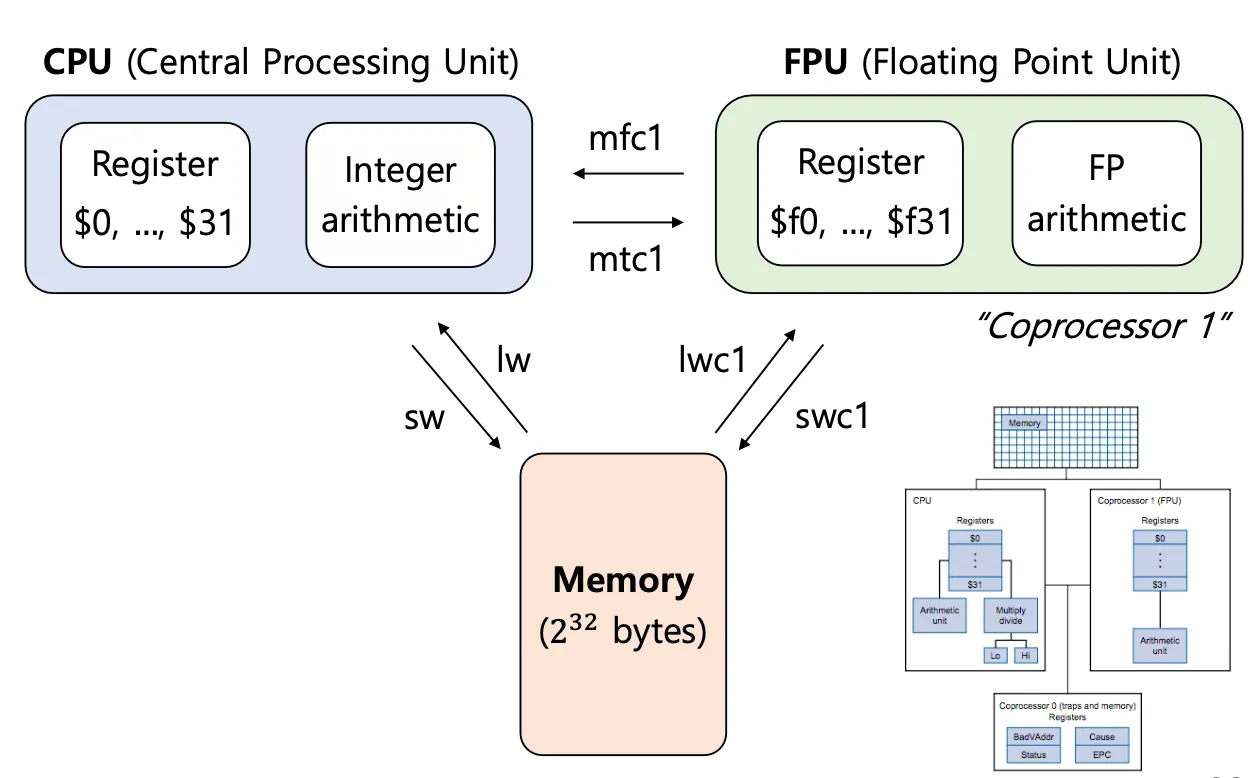
mfc0

mfc0 = move from coprocessor 0

EPC를 GPR로 가져오는 작업이다. EPC는 Error program counter로 에러가 발생한 위치를 가리키는 포인터

에러가 해결된 이후 EPC에서 가리키는 주소로 돌아가야한다.

EPC는 GPR로 가져와야하는 이유는 jr명령이 GPR에서만 동작하기 때문이다.

에러가 발생하면 CPU는 현재 실행 중인 프로그램의 주소를 EPC에 저장합니다. 이후, 예외 처리 루틴으로 점프하기 위해 EPC의 값을 GPR에 복사합니다. 에러를 해결한 후, jr 명령어를 사용하여 GPR에 저장된 주소로 복귀합니다.

Real numbers

normalized number와 not normalized number가 있다.

normalize의 정의는 소수점 앞의 값이 0이 아닌것.

normalized binary는 무조건 소수점 앞이 1이다.

과학적 표기법을 사용하면 값을 교환할때 편리하고 floating point algorithm을 적용하기 쉽고 정확하게 표현 가능하다.

fixed point = 고정소수점 = not scientific notation = 소수점 위치가 고정됨

floating point = 부동소수점 = float, double in C

Floating point의 구성요소는 exponent(지수부), fraction(소수부)가 있음.

Form: (sign, exponent, fraction) = (1, 8, 23) ⇒ float의 경우

사인비트가 0이면 -1의 0승이므로 양수라는 뜻이다.

Single Precision, Double Precision

single precision은 float이고 double precision은 double이다.

각각 32비트, 64비트를 사용한다.

더블기준으로는 (1, 11, 52)이다. 더 넓은 범위를 커버할 수 있다.

double은 2개의 레지스터를 쓰고 하나는 통째로 fraction만 저장한다.

IEEE 754

Floating point standard이다. significand = 유효숫자를 더 표현하기 위해서 normalized binary number에서 앞의 1을 빼버렸다. fraction에 사용할 수 있는 비트가 1 늘어난다. 이진수를 normalize하면 무조건 소수점 앞자리수는 1이므로 1이 생략되었다고 생각하고 표현한다.

IEEE 754 기준 fraction비트가 16개이면 1은 자동으로 표시할 수 있으니 17개의 유효숫자를 표현가능.

Biased Notation

어떤 숫자가 더 큰지 바로 알아내기 어렵기 때문에 biased notation을 사용한다

bias는 single precision 기준으로 127, double precision 기준 1023이다.

exponent에서 bias를 빼서 표현함.

bias가 없는경우 1000은 -8을 나타내고 0100은 4를 나타내기 때문에 어떤 값이 더 큰지 비교가 어렵다.

bias를 적용하면 0000이 -7이고 1000은 1이고 1110은 7이 된다.

표현 범위

00000001이 가장 작은 exponent이고 실제 값은 -126

fraction은 다 0인 경우 significand가 1.0이 된다.

bias가 적용되었으므로 1이 앞에 많을수록 큰 수가 된다.

가장 큰 수는 exponent가 11111110인 경우이고 실제 값은 127이 된다.

fraction이 전부 1이면 1.99999.. 이므로 2.0이다.

작은수 큰수 표현에 exponent 모두 1이거나 모두0인 경우는 예약되어있다

다 0인 케이스는 0으로 정의되어있고 전부 1인 케이스는 infinity로 정의함.

denormalized number = not normalized number ⇒ 소수점 앞에 0이 오는 숫자

exponent가 0이고 fraction이 존재할때1을 없애고 exponent에 1을 더해줌.

더 작은수를 표현하고 싶어서 1을 없앨수있다면 denorm으로 표현하면 훨씬 작은수까지 표현가능

normalized만 사용하면 0과 1사이를 표현할 수 있는 방법이 없기 때문에 denorm을 쓴다.

ex) -0.75를 IEEE754 binary fraction으로 바꿔라

1 + Fraction형시에 bias를 포함해서 표현한다.

음수이므로 sign bit는 1이고 1+0.5 *2의-1승 = -0.75

ex) 이 single precision으로 나타내고 있는 decimal number를 구해라.

IEEE 754에서 significand는 fraction보다 항상 1 크다. (한 자리를 더 표현할 수 있다.)

Floating Point Addition

significand가 4라는것은 fraction은 3이라는 것. = 소수점 세자리까지 표현 가능

exponent를 큰수를 기준으로 맞춘다.
1.610 * 10**-1 = 0.01610 * 10 ⇒ 0.016 (fraction이 3개)

significand끼리 더한다
9.999 + 0.016 = 10.015

normalized notation으로 바꾼다
10.015 = 1.0015 * 10**2

숫자를 fraction개수에 맞춰서 round한다.
10.0015 * 10**2 = 10.02 * 10**2

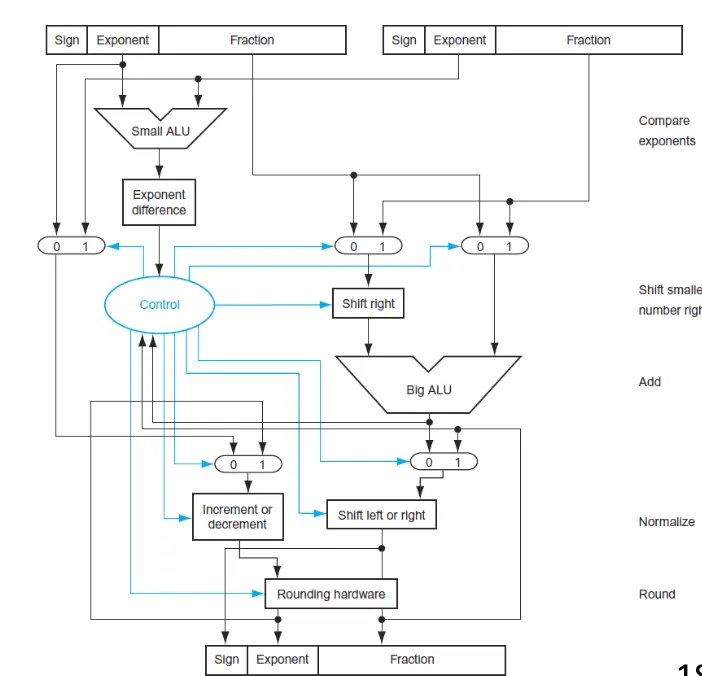
Hardware for floating-point Addition

ALU는 입력과 출력의 사이즈가 똑같아야 한다

ALU는 exponent두개를 받아서 뺄셈을 통해서 어떤 게 더 큰지 확인하고 shift smaller number right과정을 통해서 큰 수를 기준으로 맞춘다.

MUX(multiplexer)는 path를 결정해주는 스위치 역할을 한다.

bigALU는 23개짜리 숫자를 다룰 수 있어야 한다 (float의 fraction개수)

big alu에서 유효숫자를 더하고 shift left나 right를 통해서 normalized notation으로 맞춘 다음에 Rounding hardware에서 round를 수행하고 결과로 float를 반환한다.

floating point multiplication

significand가 4자리라는 것은 fraction이 3자리라는 것, 즉 소수점 3자리까지 표현한다는것.

bias를 적용한 새로운 exponent를 만든다
앞의 수의 exponent 10과 뒤의 수 exponent -5를 더하고 bias 127을 더해준다 = 132

significand끼리 곱한다.

normalized notation으로 바꾼다.
10.212 * 10**5 = 1.0212 * 10**6

fraction에 맞춰서 Rounding한다.
1.0212 ⇒ 1.021

부호를 결정한다
+1.021 * 10**6

Floating Point Instructions

floating point registers = $f0, $f1, …

single precision, double precision표현에 쓰인다.

double precision을 표현할때는 두개가 쌍으로 사용된다 $f2 ⇒ ($f2, $f3)

FP instruction은 FP레지스터에서만 동작한다.

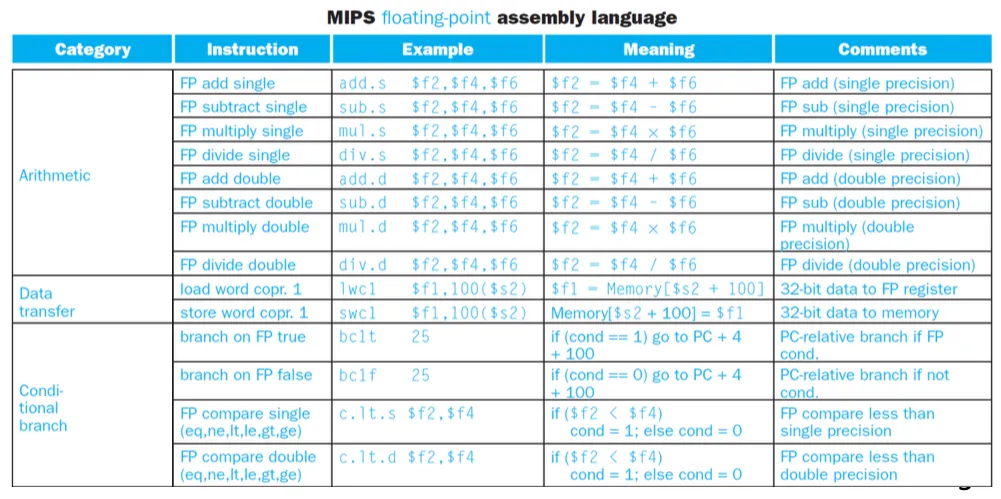
lwc1 $f4 c($sp) = 스택포인터에서 c만큼 떨어져있는 곳에서 값을 가져와서 $f4에 저장함

c1은 coprocessor 1을 말함. FPU는 coprocessor의 일종.

FPU도 32개이고 double precision을 16개 표현할 수 있다.

FPU기준으로 메모리에서 가져오는거니까 lwc1이라고 사용한다.

add.s = single precision용 add

compare하는 명령어 ⇒ c.?.s , c.?.d

c.neq.d는 double precision간에 neq를 수행한다.

bc1t ⇒ branch c1 true ⇒ true면 점프, bc1f ⇒ false면 점프

cond는 FPU안에서 관리되는 값으로 1이면 true 0이면 false이다.

floating point instruction format

산수연산은 다 r format을 가지고

lwc1같은 data transfer명령은 i format

하지만 CPU에서의 R,I format과는 다르다

FR FI ⇒ floating point용 R과 I Format

fmt = format ⇒ single이냐 double이냐를 나타냄. 16 ⇒ single 17 ⇒ double

fd는 destination

// Assume that the argument fahr in $f12 and the result in $f0
float f2c (float fahr) {
	return ((5.0/9.0)*(fahr - 32.0))
}
C++
복사

const5는 상수 5가 있는 위치(global pointer로부터 떨어져 있는 바이트수)

5.0과 9.0을 먼저 load해오고 float이므로 single precision으로 div명령 수행해서 $f16에 저장

32를 메모리에서 가져오고 $f18에 저장한 다음 fahr- 32.0을 $f18에 저장.

single precision용 mul 명령수행한다음 $f0에 저장하고 jr로 return

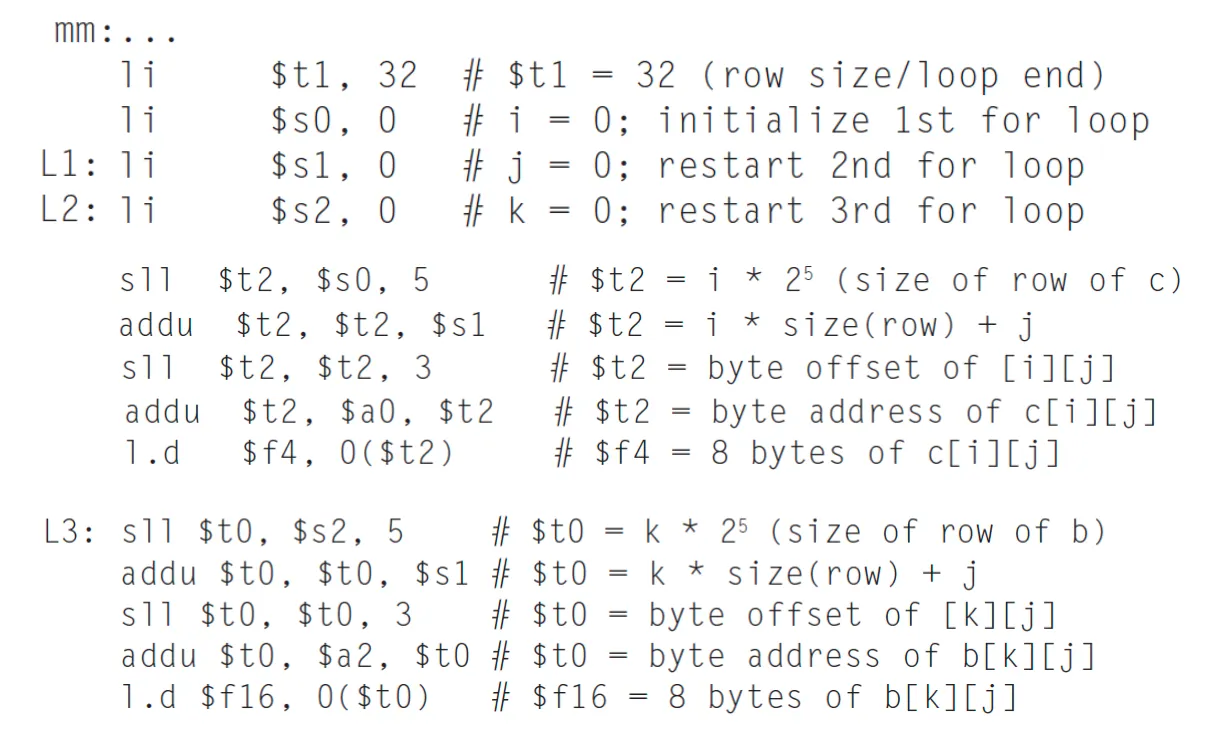
DGEMM은 fp계산 성능을 측정할 때 많이 사용하는 연산이다.

C,A, B는 모두 32*32 정방행렬. MM = matrix multiplication

li = load immediate ⇒ pseudoinstruction으로 addi $t1, $zero, 32 처럼 해석된다

lwc1 swc1은 싱글 precision용이고 ouble용은 l.d s.d

l.d, s.d는 lwc1, swc1 두번으로 해석되는 pseudoinstruction이다

matrix에서 element c[i][j]에 접근하려면 i * D + j번째 요소에 접근해야한다.(D는 row의 크기)

D = 32 = 2의5승이므로 sll $t2, $s0, 5를 수행함. 즉 i에 32를 곱한다.

그 이후에 addu로 j를 더하면 몇번째 요소인지가 나오고 sll을 통해서 alignment restriction을 맞춰주는데 double precision이기 때문에 한 칸의 크기가 8바이트라서 2의 3승을 곱해줘야한다.

2차원 배열에서 요소를 찾아가기 위해서 sll addu sll addu l.d의 과정이 반복된다.

i,j,k는 index를 가지는것이므로 음수가 나오지 않아서 addu를 사용함

li명령으로 변수들을 초기화하고, c[i][j]의 위치를 계산해서 l.d로 로드하고 L3에서는 b[k][j]를 로드하고

a[i][k]를 구하고 C + A * B에 해당하는 연산을 한 다음 F3 루프 혹은 저장하고 탈출, F2루프 혹은 탈출, F1루프 혹은 탈출하고 끝남.

Accurate Arithmetic

floating point는 52자리보다 더 정확하게 표현할수는 없기 때문에 approximation이다

좀더 실제값에 가깝게 만들기 위해서 rounding을 사용한다. rounding하려면 하드웨어가 extra bit를 보관하고 있어야 한다. IEEE754의 standard는 항상 Guard 비트와 Round 비트를 추가로 보관한다. 첫번째 비트는 guard이고 두번째 비트가 round이다. 유효숫자를 넘어서는 비트를 정확하게 표현하기 위해서 존재함.

ex) 유효숫자가 세자리인 경우 2.3656을 나타낼때 5가 guard 6이 round 비트

guard와 round가 없는 경우 0.0256에서 두자릿수까지만 남고 나머지는 잘린다.

따라서 0.02를 더하게 되므로 결과는 2.36이다.

guard bit는 leading zero인 경우에 fraction bit를 잃어버리는것을 방지하고 계산할 수 있게 해준다.

실제 반올림은 round bit에서 진행된다.

subword parallelism

오디오 샘플은 정확한 재현을 위해서 8비트를 필요로 하고 16비트 이상은 필요없다.

1 word size는 32비트니까 반만 사용해도 충분하기 때문에 subword를 사용한다.

subword는 한개의 워드를 쪼개서 halfword 등을 사용하는 것이다.

Fallacies and Pitfalls

floating point 연산은 associative하지 않다. 즉 결합법칙이 성립하지 않는다. 계산의 순서가 중요하다.
rounding하는 경우가 있기 때문이다. 이런 특성때문에 floating point는 병렬연산이 어렵고 이를 해결하기 위한 라이브러리가 존재한다.

addiu는 unsigned instruction이지만 MSB는 동일하게 sign비트이다. 즉 부호를 표현하는 비트가 필요한데 그 이유는 더하는 상수값 자체는 음수를 가질 수 있기 때문이다.  MIPS에서는 immediate field를 sign-extend한다. 

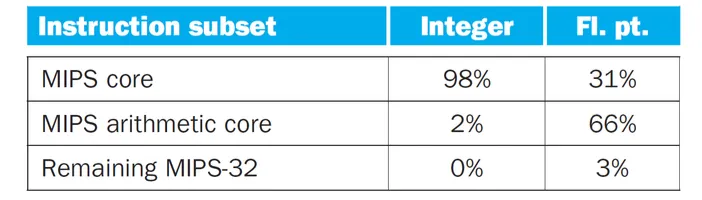
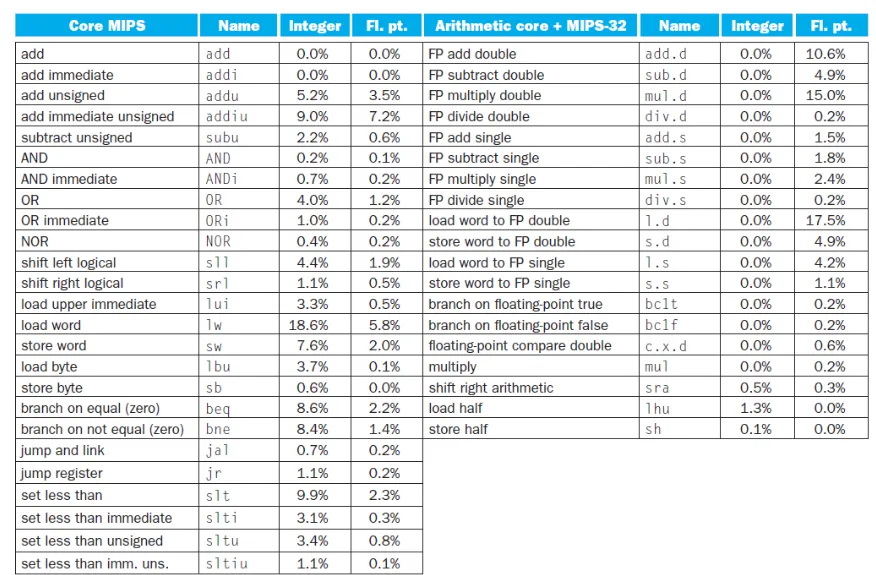
MIPS Core

사용되는 명령어는 core가 대부분을 차지한다.