Definition
재귀 호출 (Recursive Call): 메서드가 자신을 호출하는 경우.
직접 재귀 (Direct Recursion): 메서드가 직접적으로 자신을 호출하는 경우. 예를 들어, 팩토리얼 계산 같은 경우.
간접 재귀 (Indirect Recursion): 두 개 이상의 메서드가 서로를 호출하여 원래의 메서드로 돌아가는 경우. 예를 들어, 메서드 A가 메서드 B를 호출하고, B가 다시 A를 호출하는 방식.
모든 recursion은 iteration으로 표현가능하고 모든 iteration도 recursion으로 표현 가능하다.
포트란같은 언어는 recursion이 안되고 lisp같은 언어는 iteration이 없다
recursion이 iteration보다 efficiency가 낮다. 그래도 recursion을 쓰는 이유는 문제를 더 작은 문제로 만들어서 풀어서 심플하게 solution을 만들 수 있기 때문이다.
특히 트리 구조나 그래프 탐색 같은 경우에는 재귀가 코드의 가독성을 높이고, 구현을 더 간단하게 만들어준다. 포인터 변수를 사용하는 경우, 재귀는 각 단계에서 상태를 유지하는 데 유리해지므로 자연스럽게 재귀적 접근이 선호된다.
if (some condition for which answer is known) {
// base case
solution statement
}
else {
// general case
recursive function call
}
JavaScript
복사
base case: 함수가 자기 안에서 자기자신을 호출하는것을 멈추는 조건. 답이 알려져 있고 재귀없이 표현할 수 있는 경우. 재귀 알고리즘은 반드시 하나이상의 base case가 있어야 함.  general case: 문제가 자신의 더 작은 버전의 문제로 표현되는 경우
general case: 문제가 자신의 더 작은 버전의 문제로 표현되는 경우
점점 더 작은 문제로 줄여나가다가 바로 풀 수 있는 상황 = base case가 나올때까지 진행.
int Factorial ( int number )
// Pre: number is assigned and number >= 0.
{
if ( number == 0) // base case
return 1 ;
else // general case
return number * Factorial ( number - 1 ) ;
}
JavaScript
복사
// Recursive definition of power function
int Power ( int x, int n )
// Pre: n >= 0. x, n are not both zero
// Post: Function value = x raised to the power n.
{
if ( n == 0 )
return 1; // base case
else // general case
return ( x * Power ( x , n-1 ) ) ;
}
JavaScript
복사
무한 재귀 (Infinite Recursion): 함수 호출이 끝나지 않고 계속 반복되는 상황을 피해야 해. 프로그램이 멈추지 않게 만든다.
점진적 접근 (Progressive Approach): 각 재귀 호출은 알려진 답을 찾을 수 있는 상황에 점점 가까워져야 함
// base case가 두개인 경우
int Combinations(int n, int k)
{
if(k == 1) // base case 1
return n;
else if (n == k) // base case 2
return 1;
else
return(Combinations(n-1, k) + Combinations(n-1, k-1));
}
JavaScript
복사
Binary Search
BinarySearch는 반복문을 사용하여 작성할 수도 있고, 재귀를 사용하여 작성할 수도 있다.
•
반복적 접근 (Iterative Approach): 배열의 중간 요소를 확인하고, item이 중간 요소보다 작으면 왼쪽 부분을 검색하고, 크면 오른쪽 부분을 검색하는 방식으로 진행된다. fromLoc과 toLoc을 업데이트하면서 반복된다.
•
재귀적 접근 (Recursive Approach): 배열의 중간 요소를 확인한 후, item이 중간 요소보다 작으면 왼쪽 부분에 대해 재귀 호출을 하고, 크면 오른쪽 부분에 대해 재귀 호출을 한다. base case에 도달할 때까지 계속해서 자신을 호출하게 된다.
// non-recursive 방식
template <class ItemType>
void SortedType<ItemType>::RetrieveItem(ItemType &item, bool &found) {
int midPoint;
int first = 0;
int last = length - 1;
found = false;
while ((first <= last) && !found) {
midPoint = (first + last) / 2;
if (item < info[midPoint])
last = midPoint - 1;
else if (item > info[midPoint])
first = midPoint + 1;
else {
found = true;
item = info[midPoint];
}
}
}
// recursive 방식
template <class ItemType>
bool BinarySearch(ItemType info[], ItemType item, int fromLoc, int toLoc)
// Pre: info [ fromLoc . . toLoc ] sorted in ascending order
// Post: Function value = ( item in info [ fromLoc .. toLoc] )
{
int mid;
if (fromLoc > toLoc) // base case -- not found
return false;
else {
mid = (fromLoc + toLoc) / 2;
if (info[mid] == item) // base case-- found at mi
return true;
else if (item < info[mid]) // search lower half
return BinarySearch(info, item, fromLoc, mid - 1);
else // search upper half
return BinarySearch(info, item, mid + 1, toLoc);
}
}
C++
복사
Function call 동작
호출 블록에서 함수 코드로의 제어 전이가 발생한다. 함수 코드가 종료된 후에는 호출 블록의 올바른 위치로 돌아가야 하는데, 이 올바른 위치를 반환 주소 (Return Address)라고 한다.
•
제어 전이 (Transfer of Control): 함수가 호출되면 제어가 호출된 함수로 넘어가며, 함수가 실행된 후에는 원래 호출한 곳으로 돌아온다.
•
반환 주소 (Return Address): 함수 호출이 끝난 후 제어가 돌아갈 위치로, 이 주소는 함수 호출 시 스택에 저장된다.
•
런타임 스택 (Run-Time Stack): 함수가 호출될 때마다 런타임 스택이 사용되며, 각 함수 호출에 대한 활성화 레코드 (Activation Record) ⇒ 스택 프레임 (Stack Frame)이 스택에 쌓인다. 이 레코드는 함수의 매개변수, 지역 변수, 반환 주소 등을 포함한다.
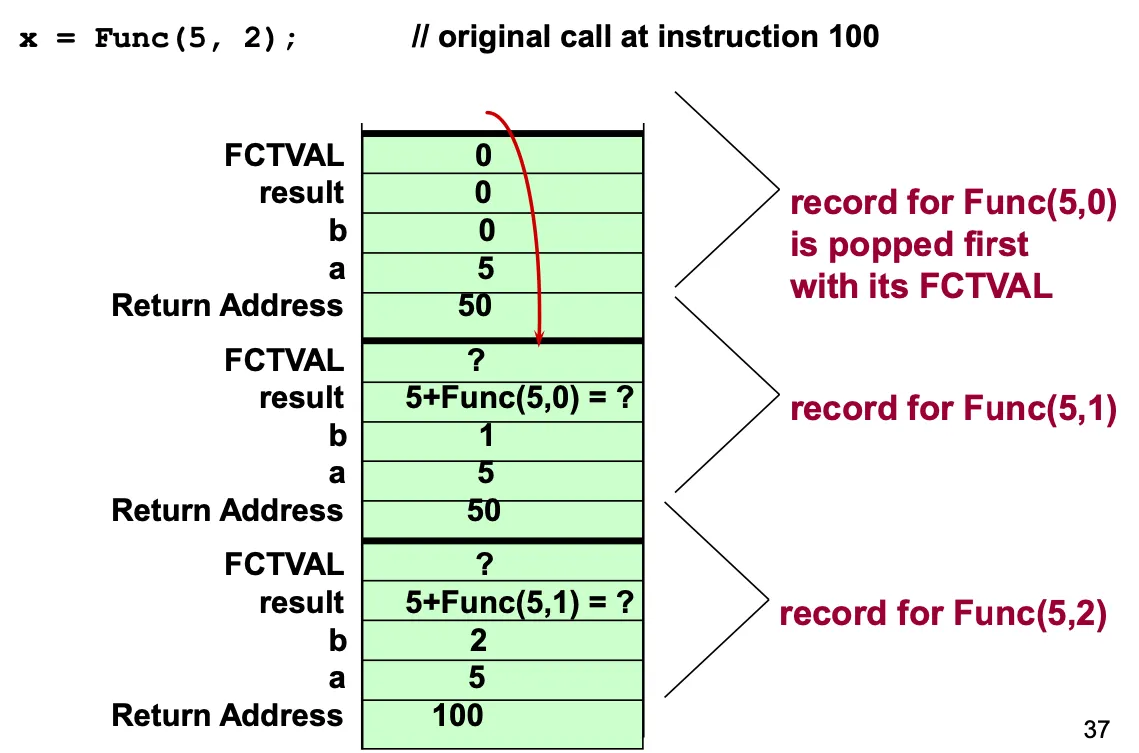
ARI
Activation Record Instance = ARI
활성화 레코드는 함수 호출의 반환주소, 함수의 매개변수, 지역변수, 반환값을 포함함.
함수가 호출될 때 새로운 활성화 레코드 인스턴스가 생성되어 런타임 스택에 push된다. 함수의 실행에 필요한 모든 정보를 담고 있으며 return이 실행되면 런타임 스택에서 pop된다. 함수의 반환값이 있다면 호출된 블록의 반환 주소로 전달된다.
InsertItem - recursive
template <class ItemType>
void Insert(NodeType<ItemType> *&location, ItemType item) {
if (location == NULL) || (item < location->info)) { // base cases
NodeType<ItemType> *tempPtr = location;
location = new NodeType<ItemType>;
location->info = item;
location->next = tempPtr;
}
else
Insert(location->next, newItem); // general case
}
template <class ItemType>
void SortedType<ItemType>::InsertItem(ItemType newItem) {
Insert(listData, newItem);
}
C++
복사
DeleteItem -recursive
template <class ItemType>
void Delete(NodeType<ItemType> *&location, ItemType item) {
if (item == location->info)) {
NodeType<ItemType> *tempPtr = location;
location = location->next;
delete tempPtr;
}
else
Delete(location->next, item);
}
template <class ItemType> void SortedType<ItemType>::DeleteItem(ItemType item) {
Delete(listData, item);
}
C++
복사
Combination - recursive
#include <iostream>
#include <vector>
void combinations(const std::vector<int>& arr, int r) {
int n = arr.size();
std::vector<std::vector<int>> result;
// 비트마스크를 사용하여 조합 생성
for (int i = 0; i < (1 << n); ++i) {
std::vector<int> combo;
for (int j = 0; j < n; ++j) {
// i의 j번째 비트가 1이면 arr[j]를 추가
if (i & (1 << j)) {
combo.push_back(arr[j]);
}
}
// 선택된 조합의 크기가 r인 경우에만 결과에 추가
if (combo.size() == r) {
result.push_back(combo);
}
}
for (const auto& c : result) {
std::cout << "{ ";
for (int num : c) {
std::cout << num << " ";
}
std::cout << "}\n";
}
}
int main() {
std::vector<int> arr = {1, 2, 3, 4};
int r = 2;
combinations(arr, r);
return 0;
}
C++
복사
Tail Recursion
tail recursion은 함수가 단일 재귀 호출만 포함하고, 그것이 함수 내에서 마지막으로 실행되는 경우를 말한다. 즉, 재귀 호출이 끝난 후 추가적인 작업이 없고, 바로 반환되는 구조이다.
tail recursion에서는 함수가 자기 자신을 호출한 후에 어떤 작업도 수행하지 않기 때문에, 컴파일러나 인터프리터가 최적화하여 반복문으로 변환할 수 있다.
이로 인해 스택 오버플로우를 방지하고, 메모리 사용을 줄일 수 있다.
tail recursion을 반복문으로 대체하면 재귀 호출을 제거할 수 있어서 성능을 개선하고 코드의 효율성을 높이는 데 도움을 준다.
재귀 호출은 함수의 매개변수와 지역 변수를 보관하기 위해 런타임 스택에 활성화 레코드를 추가한다.
활성화 레코드는 함수 호출 시 필요한 정보를 저장하는데, 재귀 호출이 함수 내에서 마지막 문장으로 실행될 경우, 함수가 종료될 때 이러한 값들을 사용하지 않게 된다.
find - tail recursion
bool ValueInList(ListType list, int value, int startIndex) {
if (list.info[startIndex] == value) // one base case
return true;
else if (startIndex == list.length - 1) // another base case
return false;
else // general case
return ValueInList(list, value, startIndex + 1);
}
C++
복사
Recursion vs Iteration
재귀 솔루션은 시간과 공간 측면에서 반복 솔루션보다 덜 효율적일 수 있다. 함수 호출이 깊어지면 스택 오버플로우와 같은 문제가 발생할 수 있다.
반복문을 사용하면 스택 메모리 사용을 줄일 수 있어 더 큰 문제를 처리하는 데 유리하다.
재귀 호출이 마지막 문장인 경우, 반복문을 사용하여 같은 작업을 수행할 수 있다.
반복 알고리즘은 루프 구조를 사용하고, 재귀 알고리즘은 분기 구조를 사용한다.
재귀는 문제의 해결을 단순화할 수 있으며, 종종 더 짧고 이해하기 쉬운 소스 코드를 생성하게 된다.
재귀를 사용해야 하는 경우
•
문제 사이즈 비해서 recursive call의 깊이가 얕은 경우
•
recursive 버전에서 하는 작업량이 nonrecursive 버전이랑 비슷한 경우 = efficiency
•
recursive버전이 더 짧고 쉬운 solution이 되는 경우
combination 계산의 경우 동일한 연산이 recursion을 사용할 때 여러번 계산되므로 효율적이지 않다.
Quick sort -recursive
template <class ItemType>
void QuickSort(ItemType values[], int first, int last) {
if (first < last) {
int splitPoint;
Split(values, first, last, splitPoint);
// values [ first ] . . values[splitPoint - 1 ] <= splitVal
// values [ splitPoint ] = splitVal
// values [ splitPoint + 1 ] . . values[ last ] > splitVal
QuickSort(values, first, splitPoint - 1);
QuickSort(values, splitPoint + 1, last);
}
}
C++
복사
퀵소트(Quick Sort) 알고리즘: 분할 정복(divide and conquer) 방식으로 동작하는 정렬 알고리즘.
평균적으로 매우 효율적이다.
퀵소트 작동 방식
기준값 선택: 배열에서 하나의 요소를 기준값(pivot)으로 선택. 기준값은 배열의 중간, 첫 번째, 마지막 요소 등 임의로 선택할 수 있다.
분할: 배열을 기준값을 기준으로 두 개의 부분 배열로 나눈다.
기준값보다 작은 요소들은 왼쪽 부분 배열에, 기준값보다 큰 요소들은 오른쪽 부분 배열에 위치하도록 한다.
재귀 정렬: 분할된 두 부분 배열에 대해 재귀적으로 퀵소트를 호출해서 배열의 크기가 1이 될 때까지 반복.
결합: 재귀 호출이 완료되면, 전체 배열이 정렬된 상태로 결합.
시간복잡도
최악의 경우 O(n^2), 평균 O(nlogn)