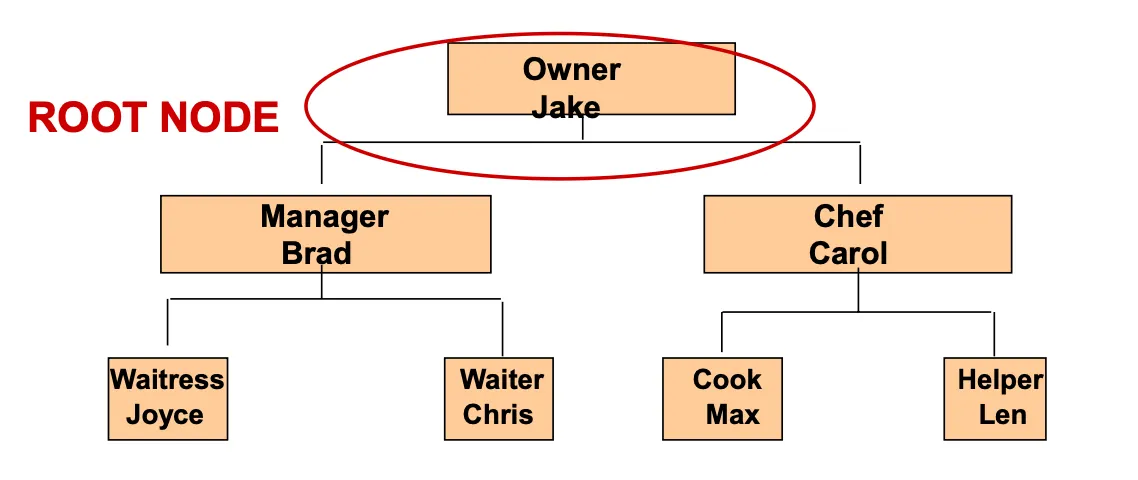
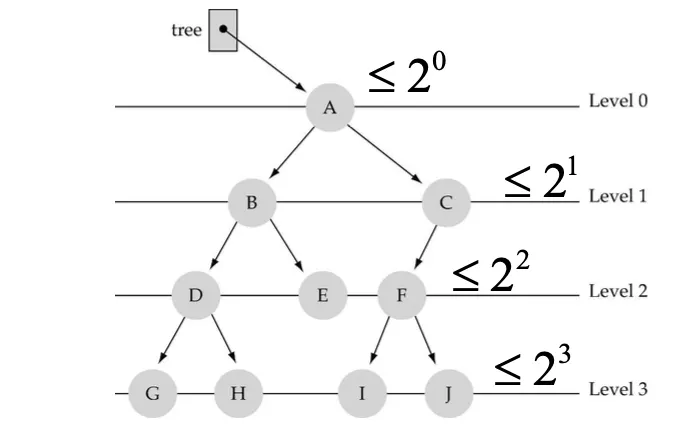
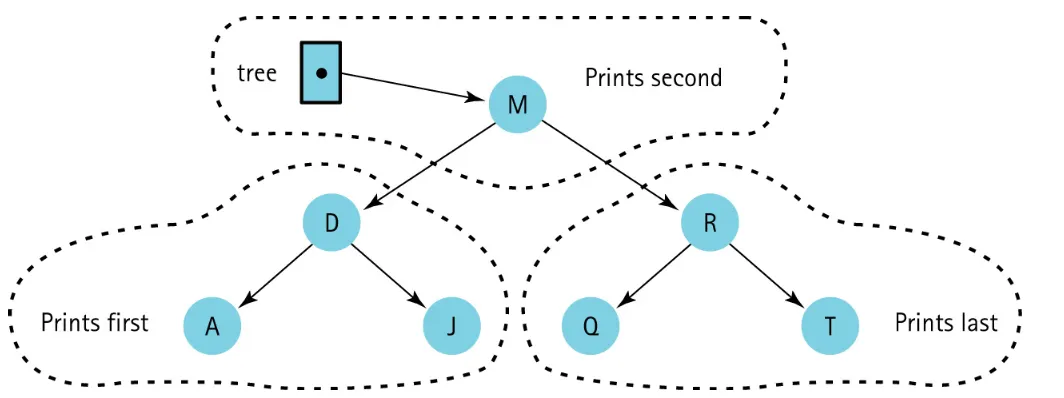
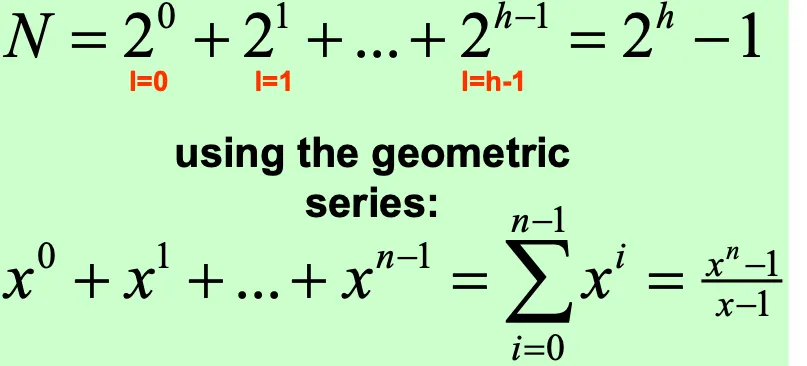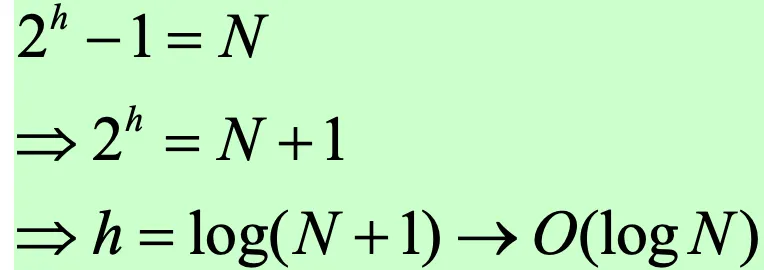Tree = root node가 있음.
root = parent가 없음.
leaf nodes = child가 없음
root = level 0
Binary tree
각 노드가 successor node(children)을 2개까지만 가질 수 있음( 없거나 한개일 수 있음 )
B와 C는 parent공유하고 있으니 sibling관계
parent보다 위는 ancestor
child보다 아래도 descendant
unary tree = list와 같음
루트로부터 특정 노드로 가는 path가 딱 하나 존재해야 tree이다.
height = number of levels
level 0~3이면 height=4
ancestor = 특정 노드에서 루트까지 가는 path에 존재하는 노드들
full tree
full binary tree의 노드수 2^height-1
시간복잡도는 logN
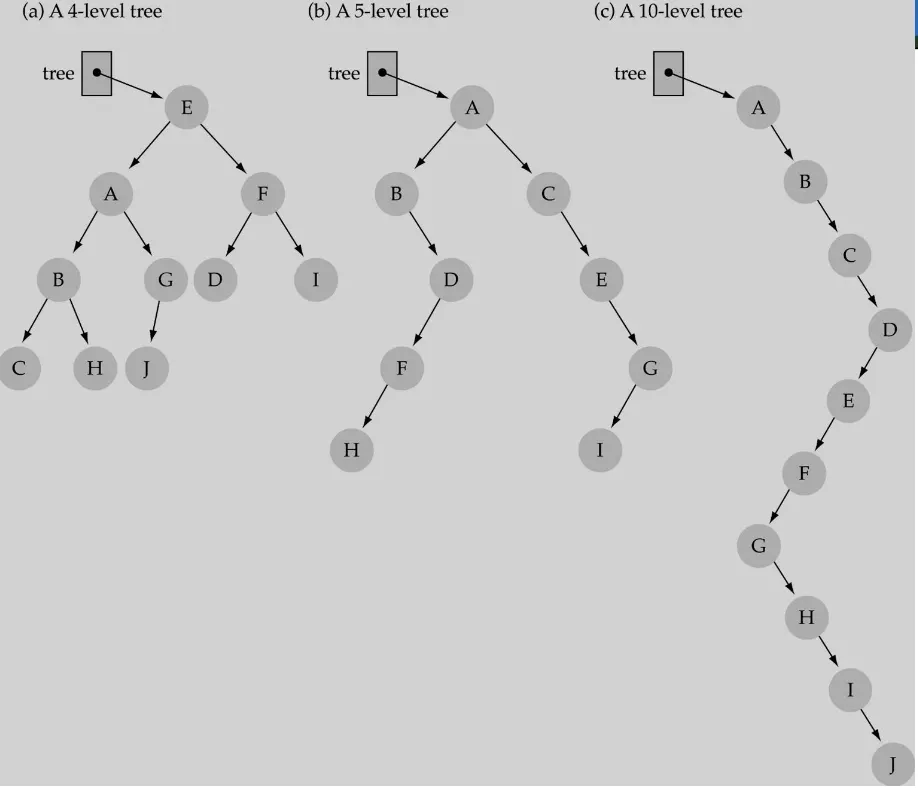
N개의 노드가 있을때 최대 height는 N (list형태)
min height는 log(N+1)
몇개의 level로 구성하냐에 따라서 height의 형태가 다르다.
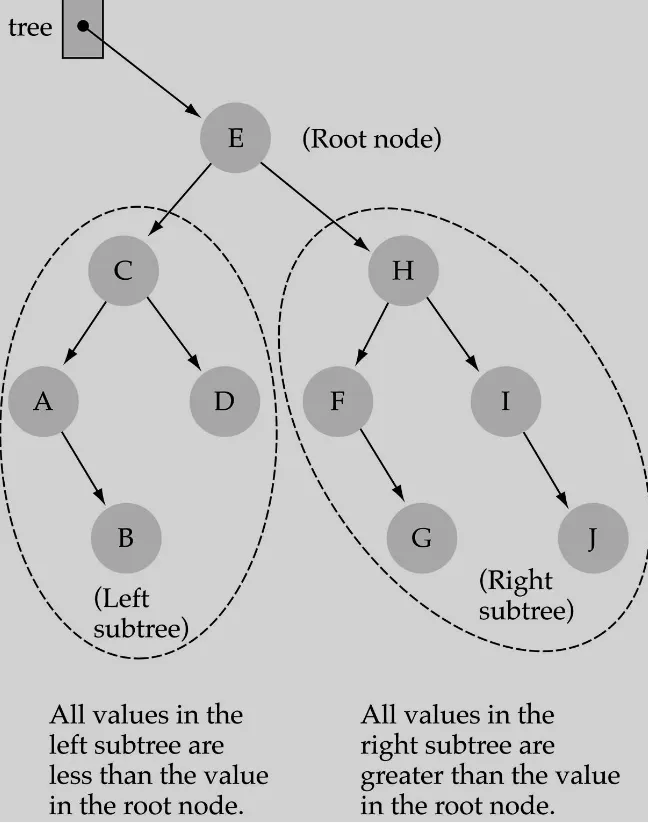
BST binary search tree
left subtree는 right subtree보다 전부 작아야함.
binary search tree의 형태는 insertion이 일어나는 순서에 따라서 다르다.
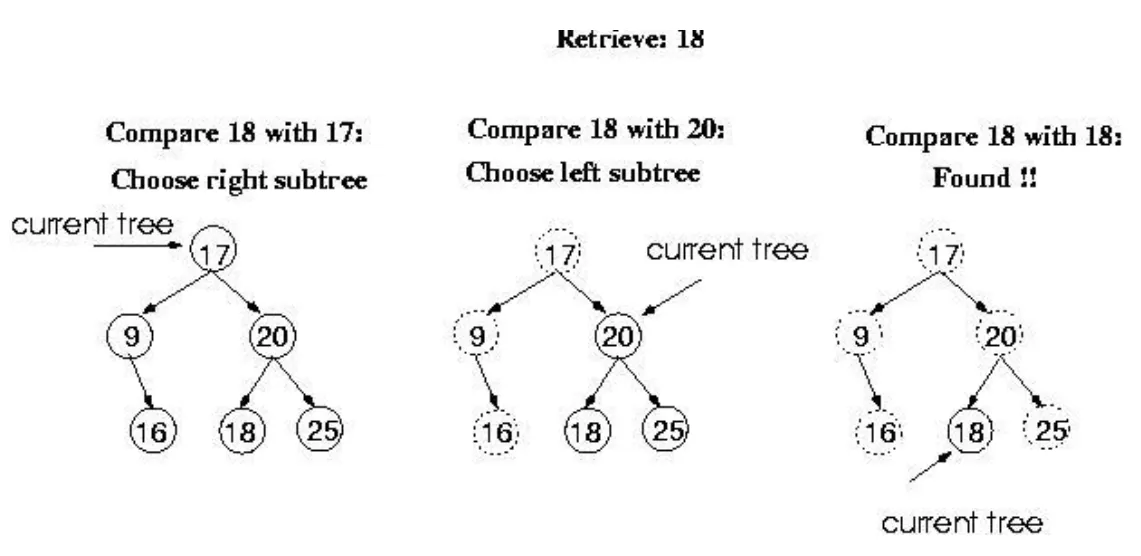
BST 탐색
1.
루트에서 시작
2.
찾는 값과 루트노드 값을 비교함
3.
값이 일치하면 찾은것. 노드가 리프노드라면 값을 찾지 못한것.
4.
값이 작을 경우 왼쪽 서브트리 탐색
5.
값이 클 경우 오른쪽 서브트리 탐색
6.
재귀적으로 반복
평균적인 시간복잡도는 O(logN)이며 worst case에 O(N)
BST Specification
#include <fstream.h>
template <class ItemType> struct TreeNode;
enum OrderType { PRE_ORDER, IN_ORDER, POST_ORDER };
template <class ItemType> class TreeType {
public:
TreeType();
~TreeType();
TreeType(const TreeType<ItemType> &);
void operator=(const TreeType<ItemType> &);
void MakeEmpty();
bool IsEmpty() const;
bool IsFull() const;
int LengthIs() const;
void RetrieveItem(ItemType &, bool &found);
void InsertItem(ItemType);
void DeleteItem(ItemType);
void ResetTree(OrderType);
void GetNextItem(ItemType &, OrderType, bool &);
void PrintTree(ofstream &) const;
private:
TreeNode<ItemType> *root;
};
//constructor
template <class ItemType> TreeType<ItemType>::TreeType() { root = NULL; }
//Destructor
void Destroy(TreeNode *&tree);
TreeType::~TreeType() { Destroy(root); }
void Destroy(TreeNode *&tree) {
if (tree != NULL) {
Destroy(tree->left);
Destroy(tree->right);
delete tree;
}
}
bool TreeType::IsFull() const {
NodeType *location;
try {
location = new NodeType;
delete location;
return false;
catch (std::bad_alloc exception)
}
{ return true; }
}
bool TreeType::IsEmpty() const { return root == NULL; }
bool TreeType::IsFull() const {
NodeType *location;
try {
location = new NodeType;
delete location;
return false;
catch (std::bad_alloc exception)
}
{ return true; }
}
bool TreeType::IsEmpty() const { return root == NULL; }
C++
복사
CountNodes
int CountNodes(TreeNode *tree)
// Recursive function that counts the nodes
{
if (tree == NULL)
return 0;
else
return CountNodes(tree->left) + CountNodes(tree->right) + 1;
}
C++
복사
RetrieveItem
void TreeType::RetrieveItem(ItemType &item, bool &found) {
Retrieve(root, item, found);
}
void Retrieve(TreeNode *tree, ItemType &item, bool &found) {
if (tree == NULL) // base case 2
found = false;
else if (item < tree->info)
Retrieve(tree->left, item, found);
else if (item > tree->info)
Retrieve(tree->right, item, found);
else // base case 1
{
item = tree->info;
found = true;
}
}
C++
복사
InsertItem
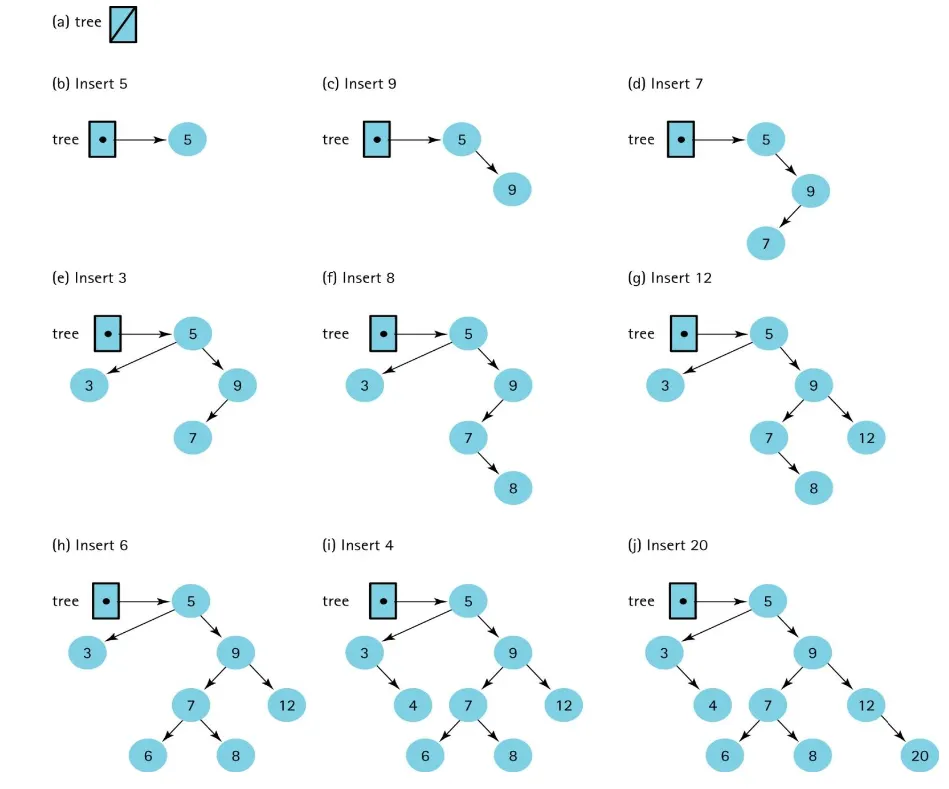
A new node is always inserted into its appropriate position in the tree as a leaf.
void Insert(TreeNode *&tree, ItemType item) {
if (tree == NULL) { // Insertion place found.
tree = new TreeNode;
tree->right = NULL;
tree->left = NULL;
tree->info = item;
} else if (item < tree->info)
Insert(tree->left, item);
else
Insert(tree->right, item);
}
C++
복사
요소를 삽입하는 순서에 따라 매우 불균형한 트리가 생성될 수 있다. 트리가 불균형하면 트리의 높이가 커져서 더 많은 노드를 방문해야 하며 O(N)의 탐색시간이 걸릴 수 있다.
균형을 유지해야 탐색, 삽입, 삭제 등의 작업을 효율적으로 할 수 있다.
Red-Black Tree등의 균형을 보장하는 고급 트리구조가 있다.
값들이 random하게 섞여 있어야 트리의 구조가 더 균형있어진다.
DeleteItem
void DeleteNode(TreeNode *&tree) {
ItemType data;
TreeNode *tempPtr;
tempPtr = tree;
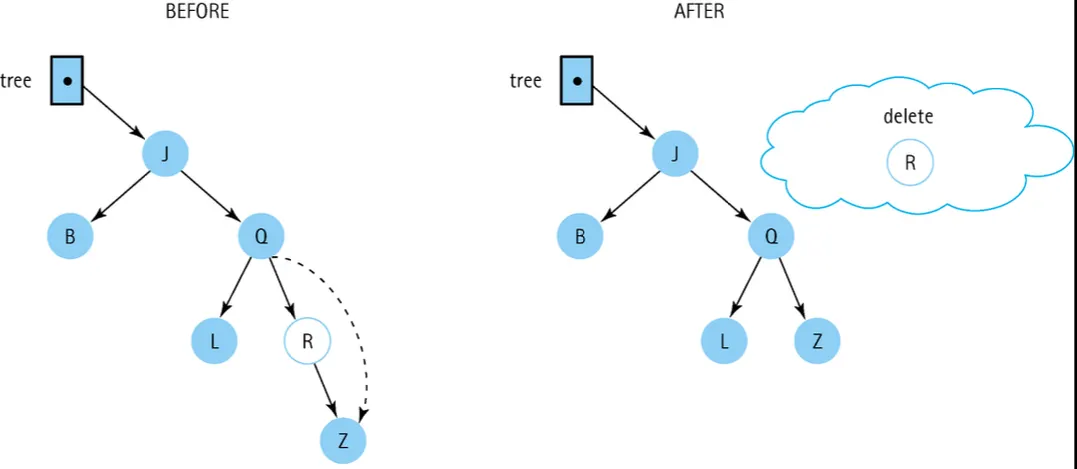
if (tree->left == NULL) { // right child
tree = tree->right;
delete tempPtr;
} else if (tree->right == NULL) { // left child
tree = tree->left;
delete tempPtr;
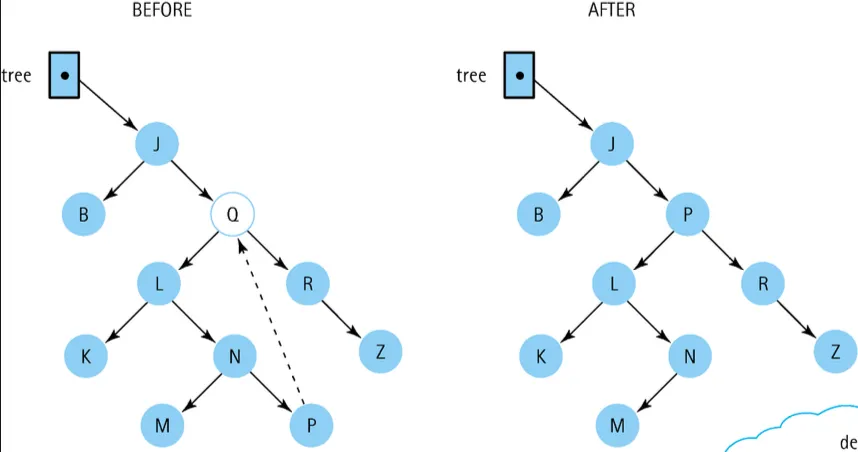
} else {
GetPredecessor(tree->left, data);
tree->info = data;
Delete(tree->left, data);
}
}
void GetPredecessor(TreeNode *tree, ItemType &data) {
while (tree->right != NULL)
tree = tree->right;
data = tree->info;
}
void Delete(TreeNode *&tree, ItemType item) {
if (item < tree->info)
Delete(tree->left, item);
else if (item > tree->info)
Delete(tree->right, item);
else
DeleteNode(tree); // Node found
}
C++
복사
DeleteNode case 3개
1.
리프 노드: 해당노드를 삭제하면 된다
2.
하나의 자식노드가 있는 노드: 삭제할 노드를 자식 노드로 대체함.
3.
두개의 자식노드가 있는 경우: 삭제할 노드의 왼쪽 서브트리에서 가장 오른쪽 노드(predecessor)를 찾아서 삭제할 노드의 값을 전임자의 값으로 대체하고 전임자를 삭제함.
right subtree의 leftmost를 사용해서 후임자로 교체해도 동작한다.
#include <iostream>
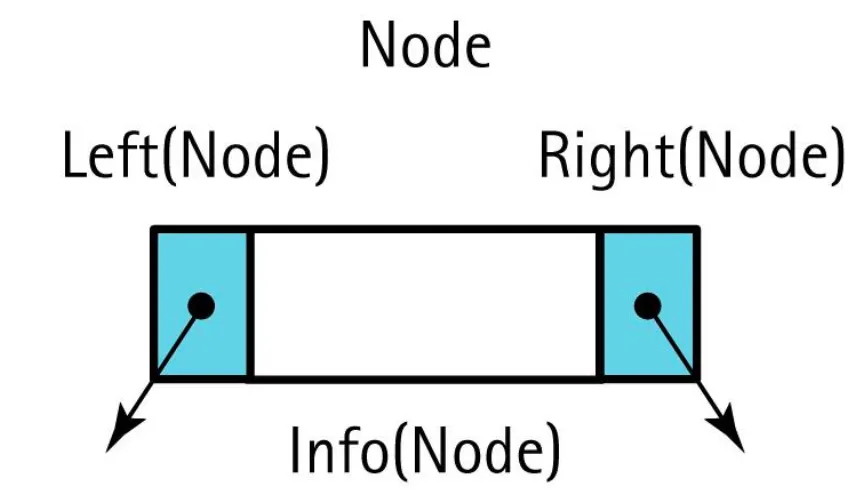
struct TreeNode {
ItemType info;
TreeNode *left;
TreeNode *right;
};
void DeleteNode(TreeNode *&tree) {
ItemType data;
TreeNode *tempPtr = tree;
if (tree->left == NULL) { // 오른쪽 자식만 있음
tree = tree->right;
delete tempPtr;
} else if (tree->right == NULL) { // 왼쪽 자식만 있음
tree = tree->left;
delete tempPtr;
} else {
// 오른쪽 서브트리의 가장 왼쪽 노드를 successor로 사용
GetSuccessor(tree->right, data);
tree->info = data; // 삭제할 노드의 정보를 successor로 대체
Delete(tree->right, data); // successor 노드 삭제
}
}
void GetSuccessor(TreeNode *tree, ItemType &data) {
while (tree->left != NULL) {
tree = tree->left; // 왼쪽으로 계속 이동
}
data = tree->info; // 가장 왼쪽 노드의 정보를 반환
}
void Delete(TreeNode *&tree, ItemType item) {
if (tree == NULL) return; // 트리가 빈 경우
if (item < tree->info) {
Delete(tree->left, item);
} else if (item > tree->info) {
Delete(tree->right, item);
} else {
DeleteNode(tree); // 노드를 찾았을 때
}
}
C++
복사
void PrintTree(TreeNode *tree, std::ofstream &outFile) {
if (tree != NULL) {
PrintTree(tree->left, outFile);
outFile << tree->info;
PrintTree(tree->right, outFile);
}
}
C++
복사
Copy Constructor
TreeType::TreeType(const TreeType &originalTree) {
CopyTree(root, originalTree.root);
}
void CopyTree(TreeNode *©, const TreeNode *originalTree) {
if (originalTree == NULL)
copy = NULL;
else {
copy = new TreeNode;
copy->info = originalTree->info;
CopyTree(copy->left, originalTree->left);
CopyTree(copy->right, originalTree->right);
}
}
C++
복사
Tree Traversal
트리 순회(Tree Traversal)는 트리의 모든 노드를 방문하는 과정
1.
중위 순회 (Inorder Traversal)
왼쪽 서브트리 → 현재 노드 → 오른쪽 서브트리
이진 탐색 트리에서는 중위 순회를 통해 노드를 정렬된 순서로 방문할 수 있다.
2.
후위 순회 (Postorder Traversal)
왼쪽 서브트리 → 오른쪽 서브트리 → 현재 노드
트리의 모든 자식 노드를 먼저 방문하고, 그 후에 부모 노드를 방문. 주로 트리를 삭제하거나 평가할 때 사용
3.
전위 순회 (Preorder Traversal)
현재 노드 → 왼쪽 서브트리 → 오른쪽 서브트리
부모 노드를 먼저 방문하고, 그 후에 자식 노드를 방문. 주로 트리의 복사나 구조를 저장할 때 사용
void InOrder(TreeNode *tree, QueType &inQue) {
if (tree != NULL) {
InOrder(tree->left, inQue);
inQue.Enqueue(tree->info);
InOrder(tree->right, inQue);
}
}
void PostOrder(TreeNode *tree, QueType &postQue) {
if (tree != NULL) {
PostOrder(tree->left, postQue);
PostOrder(tree->right, postQue);
postQue.Enqueue(tree->info);
}
}
void PreOrder(TreeNode *tree, QueType &preQue) {
if (tree != NULL) {
preQue.Enqueue(tree->info);
PreOrder(tree->left, preQue);
PreOrder(tree->right, preQue);
}
}
C++
복사
TreeType 수정
order에 따라서 RestTree, GetNextItem이 다르게 구현되어야 한다.
class TreeType {
public:
// same as before
private:
TreeNode *root;
QueType preQue;
QueType inQue;
QueType postQue;
new private data
};
void TreeType::ResetTree(OrderType order)
// Calls function to create a queue of the tree
// elements in the desired order.
{
switch (order) {
case PRE_ORDER:
PreOrder(root, preQue);
break;
case IN_ORDER:
InOrder(root, inQue);
break;
case POST_ORDER:
PostOrder(root, postQue);
break;
}
}
void TreeType::GetNextItem(ItemType &item, OrderType order, bool &finished) {
finished = false;
switch (order) {
case PRE_ORDER:
preQue.Dequeue(item);
if (preQue.IsEmpty())
finished = true;
break;
case IN_ORDER:
inQue.Dequeue(item);
if (inQue.IsEmpty())
finished = true;
break;
case POST_ORDER:
postQue.Dequeue(item);
if (postQue.IsEmpty())
finished = true;
break;
}
}
C++
복사
FindNode
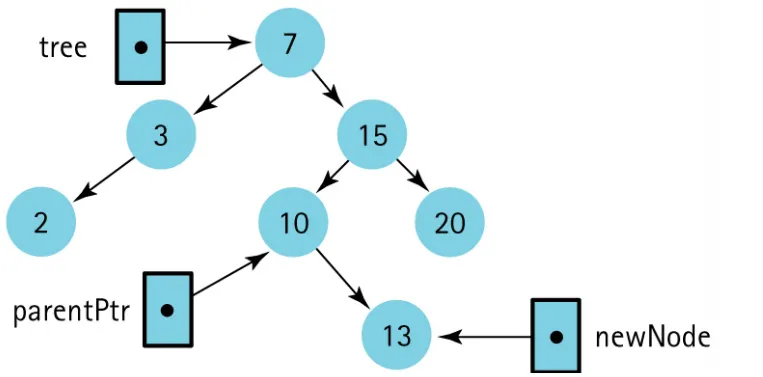
void FindNode(TreeNode *tree, ItemType item, TreeNode *&nodePtr,
TreeNode *&parentPtr) {
nodePtr = tree;
parentPtr = NULL;
bool found = false;
while (nodePtr != NULL && !found) {
if (item < nodePtr->info) {
parentPtr = nodePtr;
nodePtr = nodePtr->left;
else if (item > nodePtr->info)
}
{
parentPtr = nodePtr;
nodePtr = nodePtr->right;
}
else found = true;
}
}
C++
복사
InsertNode
nodePtr와 parentPtr는 트리 외부에 위치한 포인터.
parentPtr는 트리 외부에서 부모 노드를 가리키며,
parentPtr->left는 트리 내부의 실제 포인터로, 부모 노드의 왼쪽 자식을 가리킴.
void TreeType::InsertItem(ItemType item) {
TreeNode *newNode;
TreeNode *nodePtr;
TreeNode *parentPtr;
newNode = new TreeNode;
newNode->info = item;
newNode->left = NULL;
newNode->right = NULL;
FindNode(root, item, nodePtr, parentPtr);
if (parentPtr == NULL)
root = newNode;
else if (item < parentPtr->info)
parentPtr->left = newNode;
else
parentPtr->right = newNode;
}
C++
복사
DeleteItem
void TreeType::DeleteItem(ItemType item) {
TreeNode *nodePtr;
TreeNode *parentPtr;
FindNode(root, item, nodePtr, parentPtr);
if (nodePtr == root)
DeleteNode(root);
else if (parentPtr->left == nodePtr)
DeleteNode(parentPtr->left);
else
DeleteNode(parentPtr->right);
}
C++
복사
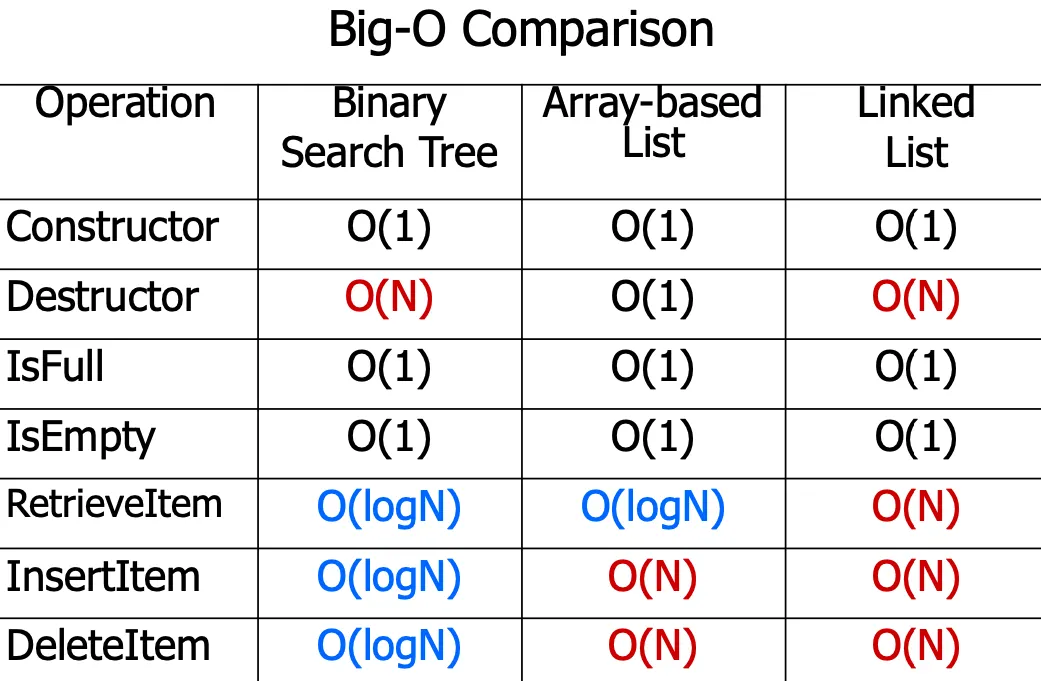
Big-O Comparsion
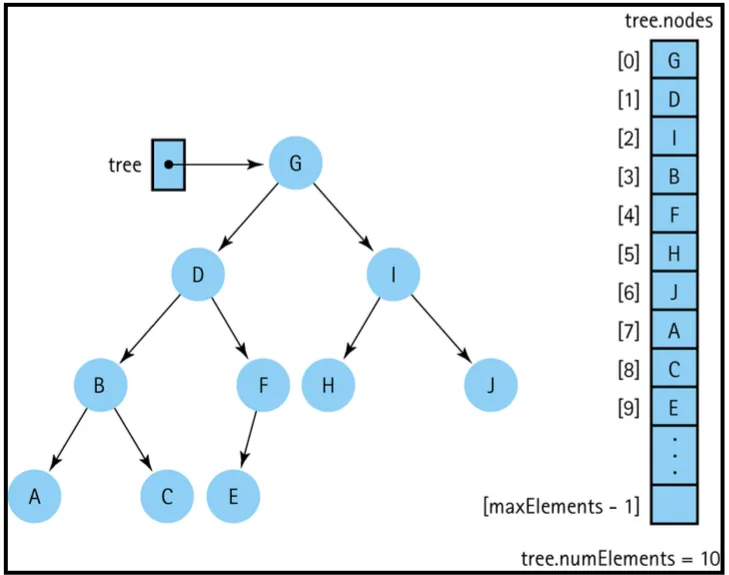
Array Representation
이진 트리는 배열로 표현될 수 있으며, 이 경우 각 노드는 배열의 인덱스를 통해 접근할 수 있다.
배열 표현의 장점은 노드 간의 관계를 쉽게 계산할 수 있다는 것.
•
현재 노드: tree.nodes[index]
•
왼쪽 자식: tree.nodes[index * 2 + 1]
•
오른쪽 자식: tree.nodes[index * 2 + 2]
•
부모 노드: tree.nodes[(index - 1) / 2]
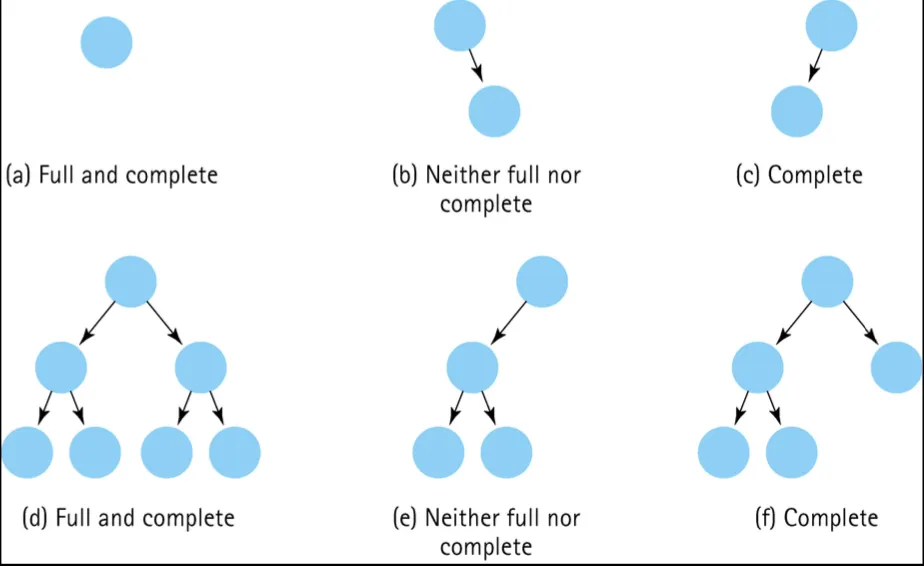
Full binary tree
모든 리프 노드가 같은 레벨에 있으며 모든 non-leaf 노드는 정확히 두개의 자식을 가지는 이진트리
Complete binary tree
모든 레벨이 완전히 채워져 있으며 마지막 레벨의 노드들은 왼쪽으로 정렬된 이진트리.