Priority Queues, Heaps and Graphs

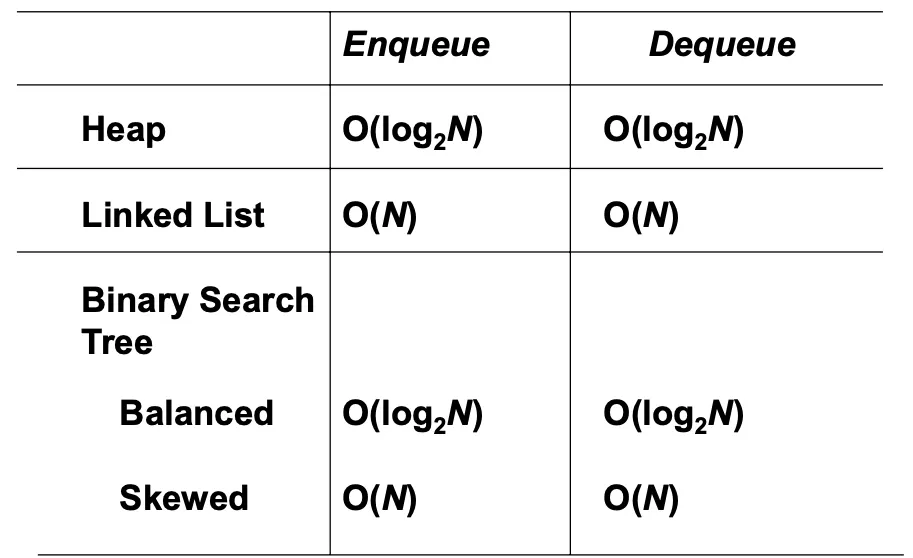
Heaps

힙(Heap)은 특정한 구조적 및 정렬 속성을 가진 이진 트리의 일종. 힙은 주로 우선순위 큐 구현에 많이 사용됨

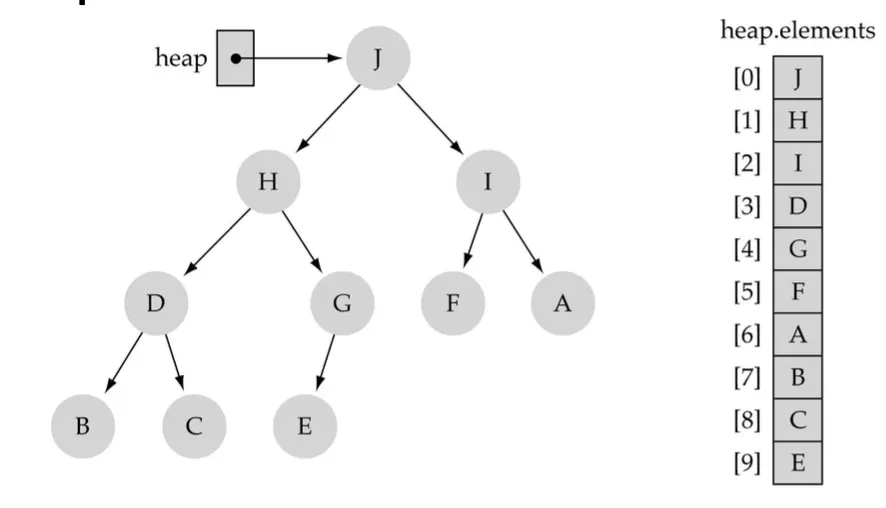
완전 이진 트리: 힙은 완전 이진 트리의 형태를 가져야 함. 이는 모든 레벨이 완전히 채워져 있으며, 마지막 레벨에서는 왼쪽부터 오른쪽으로 노드가 배치되어 있어야 한다. 이 속성 덕분에 배열로 효율적으로 표현될 수 있으며, 트리의 높이를 최소화하여 접근 및 삽입, 삭제 작업의 성능을 향상시킬 수 있음.

가장 큰 element는 root가 된다. root가 max면 max heap, min이면 min heap이다.

정렬 속성 (Order Property)

최대 힙 (Max Heap): 각 노드의 값이 그 자식 노드의 값보다 크거나 같은 경우입니다. 즉, 루트 노드가 가장 큰 값을 가지며, 모든 부모 노드는 자식 노드보다 큰 값을 가진다.

최소 힙 (Min Heap): 각 노드의 값이 그 자식 노드의 값보다 작거나 같은 경우입니다. 즉, 루트 노드가 가장 작은 값을 가지며, 모든 부모 노드는 자식 노드보다 작은 값을 가진다.

Complete binary Tree이므로 array로 표현하기 쉽다.

Heap Specification

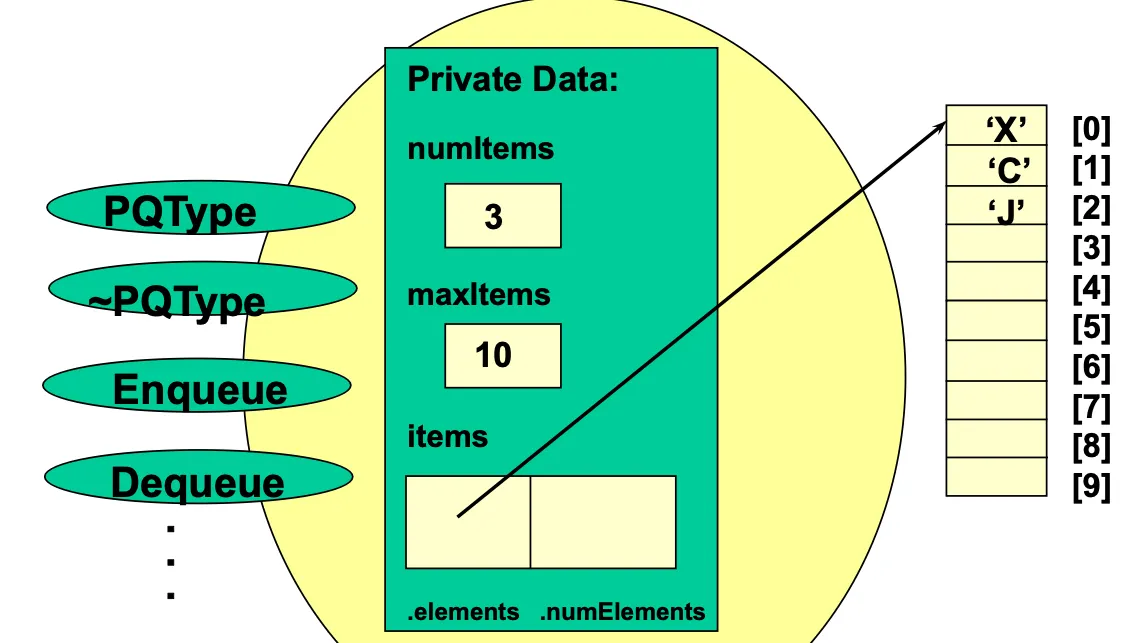
template <class ItemType> struct HeapType {
    void ReheapDown(int root, int bottom);
    void ReheapUp(int root, int bottom);
    ItemType *elements; // ARRAY to be allocated dynamically
    int numElements;
};
C++
복사

Reheap

heap조건이 깨지는 경우 다시 heap으로 만드는 것.

ReHeapDown: deleteItem 수행시에 사용됨. 삭제된 노드의 자리를 채우기 위해서 노드가 자식 노드와 비교해서 적절한 위치로 내려감.

template <class ItemType>
void HeapType<ItemType>::ReheapDown(int root, int bottom)
// Pre: root is the index of the node that may violate the
// heap order property
// Post: Heap order property is restored between root and bottom
{
    int maxChild;
    int rightChild;
    int leftChild;
    leftChild = root * 2 + 1;
    rightChild = root * 2 + 2;
    if (leftChild <= bottom) // Is there leftChild?
    {
        if (leftChild == bottom) // only one child
            maxChild = leftChld;
        else // two children
        {
            if (elements[leftChild] <= elements[rightChild])
                maxChild = rightChild;
            else
                maxChild = leftChild;
        }
        if (elements[root] < elements[maxChild]) {
            Swap(elements[root], elements[maxChild]);
            ReheapDown(maxChild, bottom);
        }
    }
}
C++
복사

ReHeapUp: InsertItem 수행시에 사용됨. 삽입된 노드가 부모노드와 비교하여 적절한 위치로 올라감.

template <class ItemType>
void HeapType<ItemType>::ReheapUp(int root, int bottom)
// Pre: bottom is the index of the node that may violate the heap
// order property. The order property is satisfied from root to
// next-to-last node.
// Post: Heap order property is restored between root and bottom
{
    int parent;
    if (bottom > root) // tree is not empty
    {
        parent = (bottom - 1) / 2;
        if (elements[parent] < elements[bottom]) {
            Swap(elements[parent], elements[bottom]);
            ReheapUp(root, parent);
        }
    }
}
C++
복사

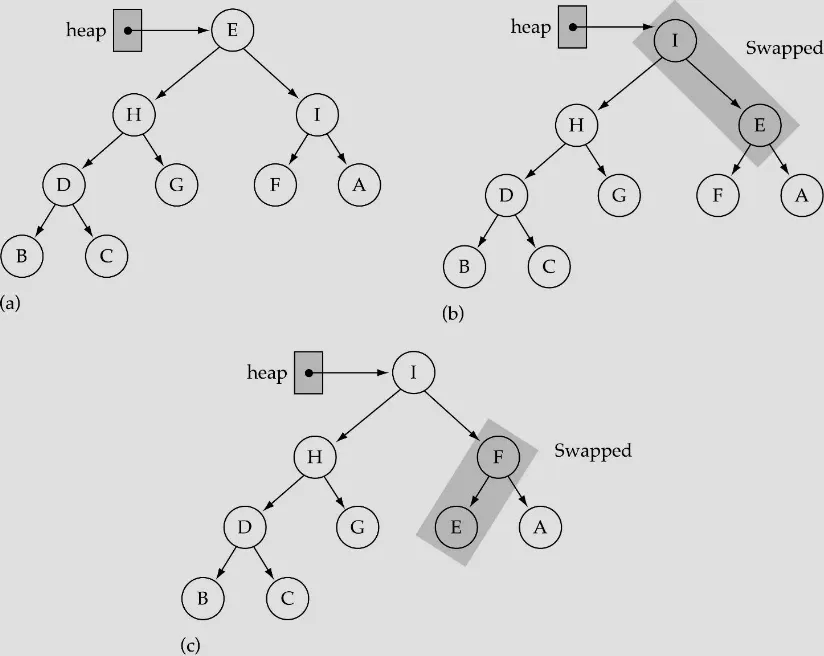
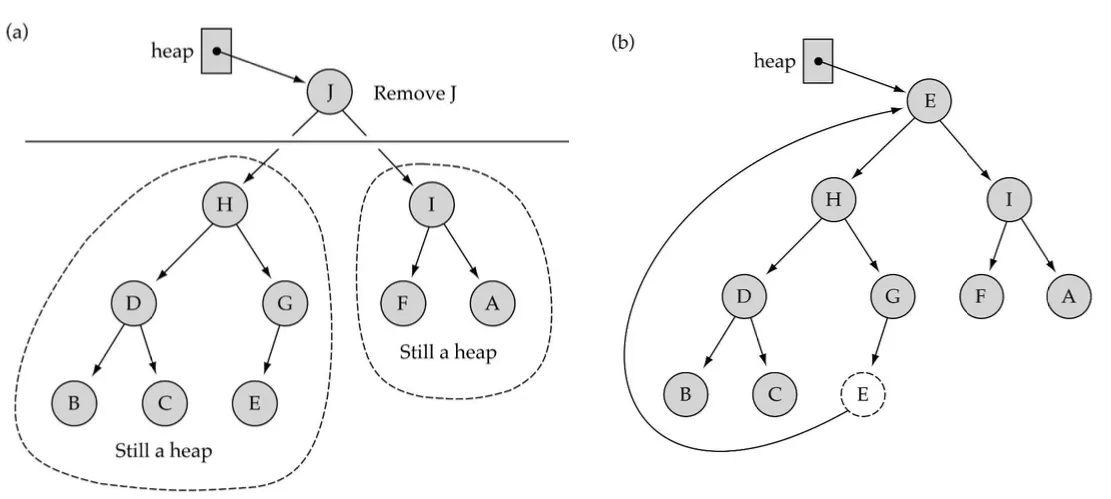
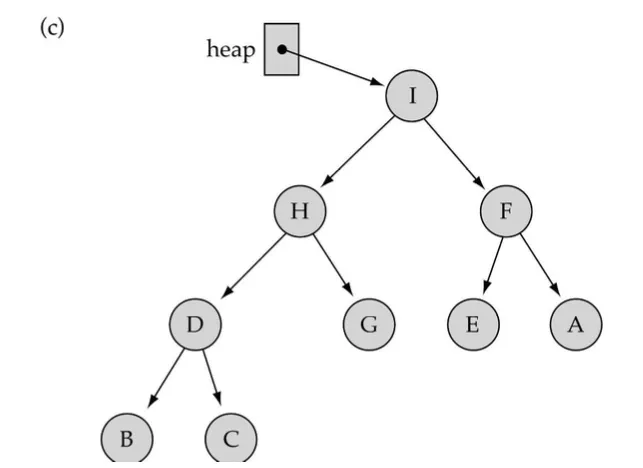
가장 큰 element 삭제

리프노드의 가장 오른쪽에 존재하는 값을 루트로 복사

가장 오른쪽 값을 삭제

ReHeapDown을 호출해서 값 수정

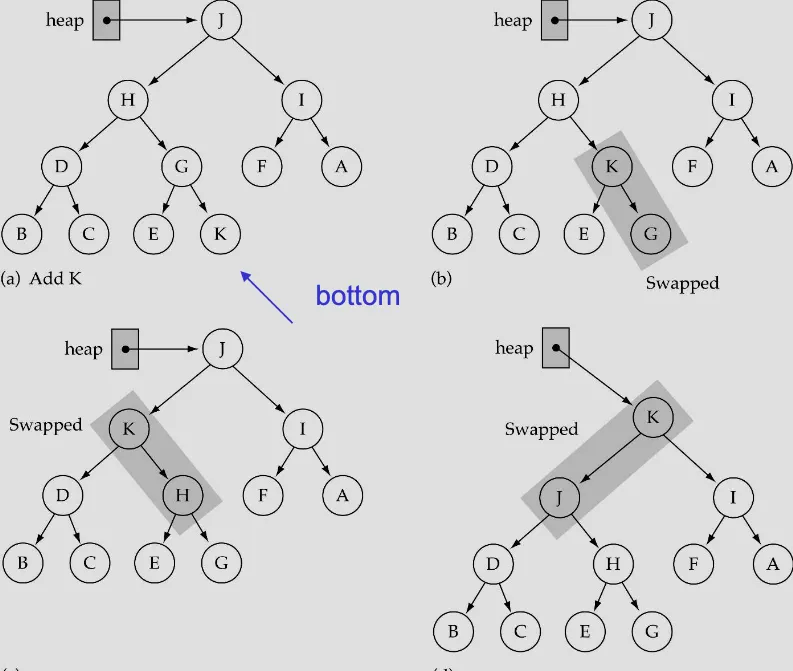
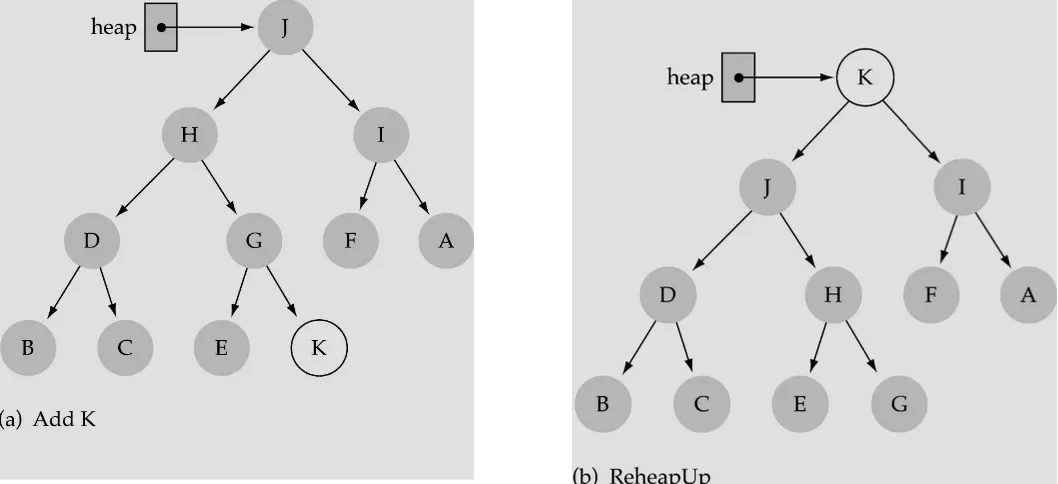
Inserting a new element into the heap

bottom leftmost에 insert

ReheapUp수행

Priority Queue

class FullPQ(){};
class EmptyPQ(){};
template <class ItemType> class PQType {
  public:
    PQType(int);
    ~PQType();
    void MakeEmpty();
    bool IsEmpty() const;
    bool IsFull() const;
    void Enqueue(ItemType newItem);
    void Dequeue(ItemType &item);

  private:
    int length;
    HeapType<ItemType> items;
    int maxItems;
};

template <class ItemType> PQType<ItemType>::PQType(int max) {
    maxItems = max;
    items.elements = new ItemType[max];
    length = 0;
}
template <class ItemType> void PQType<ItemType>::MakeEmpty() { length = 0; }
template <class ItemType> PQType<ItemType>::~PQType() {
    delete[] items.elements;
}
C++
복사

우선순위 큐는 추상 데이터타입으로 가장 높은 우선순위를 가진 요소만을 언제든지 접근할 수 있는 구조.

구현 방법

비정렬 리스트 (Unsorted List)
장점: 삽입 연산이 O(1)로 빠릅니다.
단점: 삭제(Dequeuing) 시 가장 높은 우선순위를 가진 요소를 찾기 위해 전체 리스트를 검색해야 하므로
O(N)의 시간이 필요합니다.

배열 기반 정렬 리스트 (Array-Based Sorted List)
장점: 삭제 시 가장 높은 우선순위를 가진 요소를 쉽게 찾을 수 있어 O(1)의 시간이 걸립니다.
단점: 삽입 시 리스트의 정렬 상태를 유지해야 하므로 O(N)의 시간이 필요합니다.

연결 정렬 리스트 (Linked Sorted List)
장점: 삭제 시 빠르게 접근할 수 있으며, 정렬 상태를 유지하는 동안 삭제 연산이 O(1)로 가능합니다.
단점: 삽입 시에도 정렬을 유지해야 하므로 O(N)의 시간이 걸립니다.

이진 검색 트리 (Binary Search Tree)
장점: 평균적으로 삽입과 삭제 연산이 O(logN)의 시간이 걸립니다.
단점: 최악의 경우(편향된 트리)에는 O(N)의 시간이 걸릴 수 있습니다.

힙 (Heap)
장점: 삽입과 삭제 연산 모두 O(logN)의 시간이 걸리며, 최악의 경우에도 이 시간 복잡도를 보장합니다. 
특히, 힙은 완전 이진 트리 구조이기 때문에 배열로도 쉽게 구현할 수 있습니다.
단점: 추가적인 메모리 오버헤드가 발생할 수 있습니다.

Dequeue, Enqueue

template <class ItemType> void PQType<ItemType>::Dequeue(ItemType &item) {
    if (length == 0)
        throw EmptyPQ();
    else {
        item = items.elements[0];
        items.elements[0] = items.elements[length - 1];
        length--;
        items.ReheapDown(0, length - 1);
    }
}

template <class ItemType> void PQType<ItemType>::Enqueue(ItemType newItem) {
    if (length == maxItems)
        throw FullPQ();
    else {
        length++;
        items.elements[length - 1] = newItem;
        items.ReheapUp(0, length - 1);
    }
}
C++
복사

Graphs

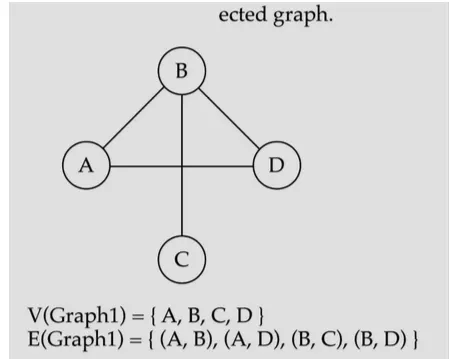
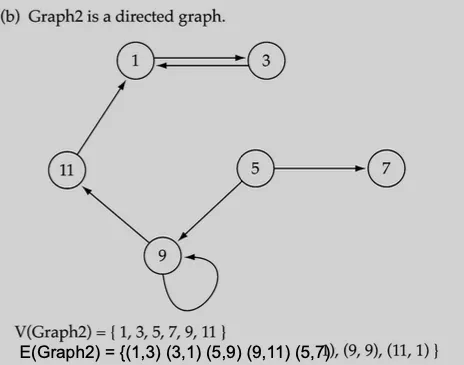
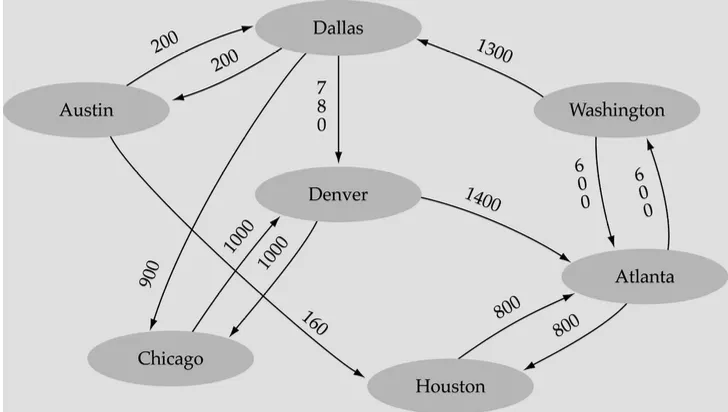
그래프(Graph)는 노드(또는 정점, vertices)와 이들 간의 관계를 나타내는 엣지(edges)로 구성된 데이터 구조로다양한 형태의 관계를 모델링하는 데 유용하다.

G = (V,E)

V(G): 유한하며 비어 있지 않은 정점의 집합. 이 정점들은 그래프의 노드이다. E(G): 정점 간의 관계를 나타내는 엣지의 집합. 각 엣지는 두 정점의 쌍으로 표현함.

Graph의 종류

•

Undirected Graph = 그래프의 엣지에 방향이 없는 경우. 

•

Directed graph(digraph) = 그래프의 엣지에 방향이 있는 경우. 각 edge들의 순서가 중요함

Trees vs Graphs

Tree는 graph의 special case. 트리는 cycle이 없는 연결된 그래프.

Graph terminology

Adjacent nodes(인접노드): 두 노드가 엣지로 연결되어 있을 때, 노드들이 서로 인접하다고 함.

Path(경로): 그래프에서 두 노드를 연결하는 정점의 순서. 경로는 정잠간의 이동을 나타내며 경로의 길이는 포함된 엣지의 개수.

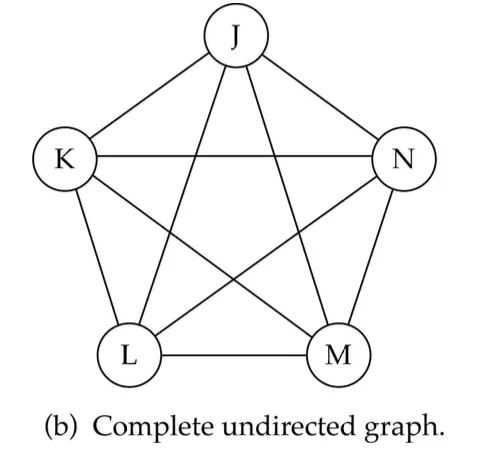
Complete Graph(완전 그래프): 모든 정점이 서로 직접 연결된 그래프. 정점의 수가 n개일 때, 완전그래프의 엣지의 수는 n(n-1)개 ⇒ directed의 경우, n(n-1)/2개 ⇒ undirected의 경우

Weighted graph(가중치 그래프): 그래프의 각 edge에 값이 부여된 그래프

Graph Implementation

Adjacency Matrix(인접행렬)

1D 배열: 정점(노드)의 집합을 나타내기 위해 1차원 배열을 사용합니다. 배열의 인덱스는 각 정점을 나타냅니다. 2D 배열: 인접 행렬을 사용하여 엣지를 나타냅니다. 이 행렬의 크기는 n×n이며, n은 정점의 수입니다. 행렬의 요소 matrix[i][j]는 정점 i와 정점 j 간의 엣지가 존재하는지 여부를 나타냄.

메모리 사용량이 많고 sparse graph인 경우 비효율적.

– Good for dense graphs --|E|~O(|V|2)

– Memory requirements: O(|V| + |E| ) = O(|V|2 )

– Connectivity between two vertices can be tested quickly

Adjacency List

정점의 집합을 나타내기 위해 1차원 배열을 사용. 각 배열 요소는 해당 정점에 대한 인접 리스트의 시작점을 가리킴

– Good for sparse graphs -- |E|~O(|V|)

– Memory requirements: O(|V| + |E|)=O(|V|)

– Vertices adjacent to another vertex can be found quickly

Graph Specification - Adjacancy Matrix

// Adjacency Matrix 기반
const int NULL_EDGE = 0;
template <class VertexType> class GraphType {
  public:
    GraphType(int);
    ~GraphType();
    void MakeEmpty();
    bool IsEmpty() const;
};
bool IsFull() const;
void AddVertex(VertexType);
void AddEdge(VertexType, VertexType, int);
int WeightIs(VertexType, VertexType);
void GetToVertices(VertexType, QueType<VertexType> &);
void ClearMarks();
void MarkVertex(VertexType);
bool IsMarked(VertexType) const;

template <class VertexType> GraphType<VertexType>::GraphType(int maxV) {
    numVertices = 0;
    maxVertices = maxV;
    vertices = new VertexType[maxV];
    edges = new int[maxV];
    for (int i = 0; i < maxV; i++)
        edges[i] = new int[maxV];
    marks = new bool[maxV];
}
template <class VertexType> GraphType<VertexType>::~GraphType() {
    delete[] vertices;
    for (int i = 0; i < maxVertices; i++)
        delete[] edges[i];
    delete[] edges;
    delete[] marks;
}
void GraphType<VertexType>::AddVertex(VertexType vertex) {
    vertices[numVertices] = vertex;
    for (int index = 0; index < numVertices; index++) {
        edges[numVertices][index] = NULL_EDGE;
        edges[index][numVertices] = NULL_EDGE;
    }
    numVertices++;
    template <class VertexType>
    void GraphType<VertexType>::AddEdge(VertexType fromVertex,
                                        VertexType toVertex, int weight)
}
{
    int row;
    int column;
    row = IndexIs(vertices, fromVertex);
    col = IndexIs(vertices, toVertex);
    edges[row][col] = weight;
}
template <class VertexType>
int GraphType<VertexType>::WeightIs(VertexType fromVertex,
                                    VertexType toVertex) {
    int row;
    int column;
    row = IndexIs(vertices, fromVertex);
    col = IndexIs(vertices, toVertex);
    return edges[row][col];
}
C++
복사

Graph Specification - Adjacency list

#include <iostream>
#include <vector>
#include <list>
#include <unordered_map>
#include <queue>

template <class VertexType>
class GraphType {
public:
    GraphType(int maxV);
    ~GraphType();
    void MakeEmpty();
    bool IsEmpty() const;
    bool IsFull() const;
    void AddVertex(VertexType vertex);
    void AddEdge(VertexType fromVertex, VertexType toVertex, int weight);
    int WeightIs(VertexType fromVertex, VertexType toVertex);
    void GetToVertices(VertexType vertex, std::queue<VertexType>& vertexQueue);
    void ClearMarks();
    void MarkVertex(VertexType vertex);
    bool IsMarked(VertexType vertex) const;

private:
    int numVertices;
    int maxVertices;
    std::unordered_map<VertexType, std::list<std::pair<VertexType, int>>> edges; // Adjacency list
    std::unordered_map<VertexType, bool> marks; // Marks for vertices

    int IndexIs(VertexType vertex);
};

template <class VertexType>
GraphType<VertexType>::GraphType(int maxV) : maxVertices(maxV), numVertices(0) {}

template <class VertexType>
GraphType<VertexType>::~GraphType() {
    MakeEmpty();
}

template <class VertexType>
void GraphType<VertexType>::MakeEmpty() {
    edges.clear();
    marks.clear();
    numVertices = 0;
}

template <class VertexType>
bool GraphType<VertexType>::IsEmpty() const {
    return numVertices == 0;
}

template <class VertexType>
bool GraphType<VertexType>::IsFull() const {
    return numVertices == maxVertices;
}

template <class VertexType>
void GraphType<VertexType>::AddVertex(VertexType vertex) {
    if (IsFull()) {
        std::cerr << "Graph is full!" << std::endl;
        return;
    }
    if (edges.find(vertex) == edges.end()) {
        edges[vertex] = std::list<std::pair<VertexType, int>>();
        numVertices++;
    }
}

template <class VertexType>
void GraphType<VertexType>::AddEdge(VertexType fromVertex, VertexType toVertex, int weight) {
    if (edges.find(fromVertex) != edges.end() && edges.find(toVertex) != edges.end()) {
        edges[fromVertex].emplace_back(toVertex, weight);
        edges[toVertex].emplace_back(fromVertex, weight); // For undirected graph
    }
}

template <class VertexType>
int GraphType<VertexType>::WeightIs(VertexType fromVertex, VertexType toVertex) {
    if (edges.find(fromVertex) != edges.end()) {
        for (const auto& pair : edges[fromVertex]) {
            if (pair.first == toVertex) {
                return pair.second; // Return weight
            }
        }
    }
    return 0; // If no edge exists
}

template <class VertexType>
void GraphType<VertexType>::GetToVertices(VertexType vertex, std::queue<VertexType>& vertexQueue) {
    if (edges.find(vertex) != edges.end()) {
        for (const auto& pair : edges[vertex]) {
            vertexQueue.push(pair.first); // Push adjacent vertices into the queue
        }
    }
}

template <class VertexType>
void GraphType<VertexType>::ClearMarks() {
    marks.clear();
}

template <class VertexType>
void GraphType<VertexType>::MarkVertex(VertexType vertex) {
    marks[vertex] = true; // Mark the vertex
}

template <class VertexType>
bool GraphType<VertexType>::IsMarked(VertexType vertex) const {
    auto it = marks.find(vertex);
    return it != marks.end() && it->second; // Check if marked
}

// Example IndexIs function (not used in adjacency list implementation)
template <class VertexType>
int GraphType<VertexType>::IndexIs(VertexType vertex) {
    // Implementation of IndexIs can be added if needed for specific purposes
    return -1; // Placeholder
}
C++
복사

Graph Searching

두 노드간의 경로를 찾는 문제. DFS, BFS가 있음

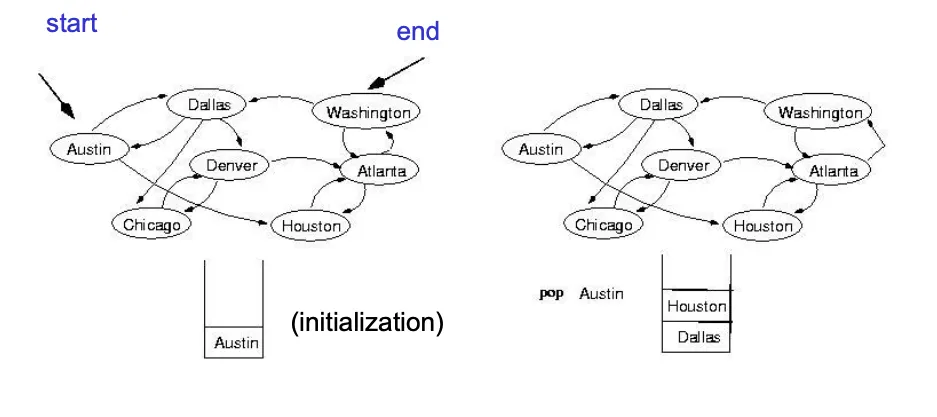
DFS (Depth First Search)

한가지 경로를 선택한 후 그 경로를 가능한 깊게 탐색함. 현재노드에서 자식 노드로 이동하며 더 이상 진행할 수 없을때까지 내려가고 더 이상 갈 수 없는 노드에 도달하면 이전 노드로 돌아가 다른 경로 탐색.

스택을 사용해서 효율적으로 구현할 수 있다.

template <class ItemType>
void DepthFirstSearch(GraphType<VertexType> graph, VertexType startVertex,
                      VertexType endVertex) {
    StackType<VertexType> stack;
    QueType<VertexType> vertexQ;
    bool found = false;
    VertexType vertex;
    VertexType item;
    graph.ClearMarks();
    stack.Push(startVertex);
    do {
        stack.Pop(vertex);
        if (vertex == endVertex)
            found = true;
        else {
            if (!graph.IsMarked(vertex)) {
                graph.MarkVertex(vertex);
                graph.GetToVertices(vertex, vertexQ);
                while (!vertexQ.IsEmpty()) {
                    vertexQ.Dequeue(item);
                    if (!graph.IsMarked(item))
                        stack.Push(item);
                }
            }
        }
    } while (!stack.IsEmpty() && !found);
    if (!found)
        cout << "Path not found" << endl;
}

template <class VertexType>
void vertex, GraphType<VertexType>::GetToVertices(
                 VertexType QueTye<VertexType> &adjvertexQ) {
    int fromIndex;
    int toIndex;
    fromIndex = IndexIs(vertices, vertex);
    for (toIndex = 0; toIndex < numVertices; toIndex++)
        if (edges[fromIndex][toIndex] != NULL_EDGE)
            adjvertexQ.Enqueue(vertices[toIndex]);
}
C++
복사

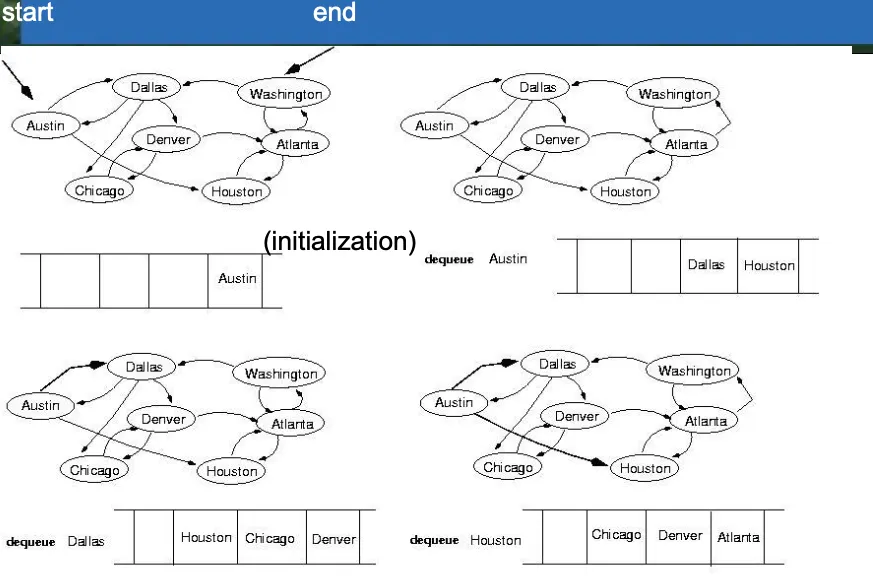
BFS (Breadth First Search)

너비우선탐색은 특정 노드에서 시작해서 모든 노드를 레벨별로 방문함. 레벨 우선 탐색.

한 레벨의 모든 노드를 방문하고 다음 레벨로 넘어간다. BFS는 큐를 사용해서 구현할 수 있다.

push전에 마킹을 수행하는게 좋다. 마크 체크 안하면 스택에 똑같은애가 여러번 들어갈 수 있다.

template <class VertexType>
void BreadthFirtsSearch(GraphType<VertexType> graph, VertexType startVertex,
                        VertexType endVertex);
{
    QueType<VertexType> queue;
    QueType<VertexType> vertexQ; //
    bool found = false;
    VertexType vertex;
    VertexType item;
    graph.ClearMarks();
    queue.Enqueue(startVertex);
    do {
        queue.Dequeue(vertex);
        if (vertex == endVertex)
            found = true;
        else {
            if (!graph.IsMarked(vertex)) {
                graph.MarkVertex(vertex);
                graph.GetToVertices(vertex, vertexQ);
                while (!vertxQ.IsEmpty()) {
                    vertexQ.Dequeue(item);
                    if (!graph.IsMarked(item))
                        queue.Enqueue(item);
                }
            }
        }
    } while (!queue.IsEmpty() && !found);
    if (!found)
        cout << "Path not found" << endl;
}
C++
복사

Shortest path problem

source vertex에서 destination vertex까지 경로의 total weigth의 합이 가장 작은 path를 구하는 문제

다익스트라, 벨만포드 알고리즘 등이 있음.

그래프에 가중치가 없으면 BFS가 shortest path를 구하는 알고리즘으로 사용될 수 있음