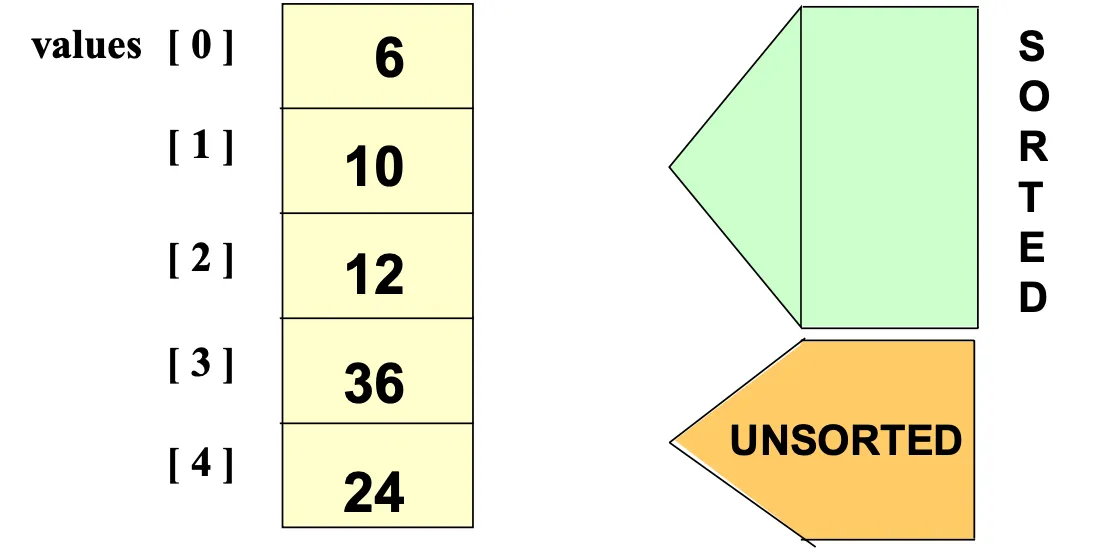
정렬: 배열에 저장된 요소들을 오름차순이나 내림차순으로 재배치하는 과정.
Selection sort( 선택정렬 )
배열을 정렬된 부분과 정렬되지 않은 부분으로 나눠서 매 회차마다 정렬되지 않은 부분에서 가장 작은 요소를 찾아서 정렬된 부분의 끝에 추가함. 시간복잡도 O(N^2)
template <class ItemType>
int MinIndex(ItemType values[], int start, int end)
// Post: Function value = index of the smallest value
// in values [start] . . values [end].
{
int indexOfMin = start;
for (int index = start + 1; index <= end; index++)
if (values[index] < values[indexOfMin])
indexOfMin = index;
return indexOfMin;
}
template <class ItemType>
void SelectionSort(ItemType values[], int numValues)
// Post: Sorts array values[0 . . numValues-1 ]
// into ascending order by key
{
int endIndex = numValues - 1;
for (int current = 0; current < endIndex; current++)
Swap(values[current], values[MinIndex(values, current, endIndex)]);
}
C++
복사
Bubble sort
배열의 인접한 요소들을 비교하고 필요에 따라 교환하여 정렬하는 알고리즘. 가장 큰 요소가 배열의 끝으로 버블링되어 올라간다. 시간복잡도 O(N^2)
template <class ItemType> void BubbleSort(ItemType values[], int numValues) {
int current = 0;
while (current < numValues - 1) {
BubbleUp(values, current, numValues - 1);
current++;
}
}
template <class ItemType>
void BubbleUp(ItemType values[], int startIndex, int endIndex)
{
for (int index = endIndex; index > startIndex; index--)
if (values[index] < values[index - 1])
Swap(values[index], values[index - 1]);
}
C++
복사
Insertion Sort
삽입정렬은 배열의 요소를 하나씩 정렬된 부분에 삽입하여 정렬하는 방법. 카드게임에서 카드를 정렬하는 방식과 유사함. 시간복잡도 O(N^2)
template <class ItemType>
void InsertItem(ItemType values[], int start, int end) {
bool finished = false;
int current = end;
bool moreToSearch = (current != start);
while (moreToSearch && !finished) {
if (values[current] < values[current - 1]) {
Swap(values[current], values[current - 1]);
current--;
moreToSearch = (current != start);
} else
finished = true;
}
}
template <class ItemType> void InsertionSort(ItemType values[], int numValues) {
// ascending order by key
for (int count = 0; count < numValues; count++)
InsertItem(values, 0, count);
}
C++
복사
Complex Sorts
선택, 버블, 삽입정렬은 simple한 sort알고리즘으로 시간복잡도가 O(N^2)이지만 Quick, Merge, Heap Sort는 O(nlogn)이다.
Heap Sort
힙 정렬은 힙 자료구조를 사용해서 배열을 정렬한다.
1.
루트를 배열의 끝에 있는 정렬된 부분으로 이동시킨다. 이를 위해서 루트 element를 배열의 마지막 요소와 교환한다.
2.
루트에 있는 요소를 제거한 후 나머지 요소로 힙을 재구성한다. 이 과정에서 새로운 루트가 올바른 위치로 이동한다→ 다음으로 큰 요소가 루트에 온다
3.
이 과정을 정렬되지 않은 요소가 없을때까지 반복한다.
힙 정렬은 추가적인 메모리 공간 없이 정렬이 가능하다.
template <class ItemType>
void HeapSort(ItemType values[], int numValues)
// Post: Sorts array values[ 0 . . numValues-1 ] into
// ascending order by key
{
int index;
// Convert array values[0..numValues-1] into a heap
for (index = numValues / 2 - 1; index >= 0; index--)
ReheapDown(values, index, numValues - 1);
// Sort the array.
for (index = numValues - 1; index >= 1; index--) {
Swap(values[0], values[index]);
ReheapDown(values, 0, index - 1);
}
}
template <class ItemType>
void ReheapDown(ItemType values[], int root, int bottom)
{
int maxChild;
int rightChild;
int leftChild;
leftChild = root * 2 + 1;
rightChild = root * 2 + 2;
if (leftChild <= bottom) // ReheapDown continued
{
if (leftChild == bottom)
maxChild = leftChild;
else {
if (values[leftChild] <= values[rightChild])
maxChild = rightChild;
else
maxChild = leftChild;
if (values[root] < values[maxChild])
}
{
Swap(values[root], values[maxChild]);
ReheapDown(maxChild, bottom);
}
}
}
C++
복사
힙의 리프노드는 이미 heap이라고 볼 수 있다. 부모노드가 자식노드보다 커야하는데 자식이 없다.
한칸 위로 올라가면 reheap한번에 heap이 된다.
또 한칸씩 올라가면서 reheap을 수행해서 root까지 간다.
heap의 높이는 O(logN)이다.
(N/2) * O(log N) compares to create original heap
(N-1) * O(log N) compares for the sorting loop
= O ( N * log N) compares total
Quick Sort
// Recursive quick sort algorithm
template <class ItemType>
void QuickSort(ItemType values[], int first, int last)
// Pre: first <= last
// Post: Sorts array values[ first . . last ] into ascending order
{
if (first < last) // general case
{
int splitPoint;
Split(values, first, last, splitPoint);
// values [first]..values[splitPoint - 1] <= splitVal
// values [splitPoint] = splitVal
// values [splitPoint + 1]..values[last] > splitVal
QuickSort(values, first, splitPoint - 1);
QuickSort(values, splitPoint + 1, last);
}
};
C++
복사
1.
주어진 배열에서 pivot값(splitVal)을 선택
2.
배열의 모든 요소를 피벗과 비교해서 피벗보다 작거나 같은 값은 왼쪽에, 큰값은 오른쪽에 배치함.
N번의 비교가 발생함.
3.
피벗을 제외한 왼쪽과 오른쪽 부분에 대해서 같은 과정을 재귀적으로 반복.
4.
배열의 크기가 1이하일 경우 이미 정렬된 상태
시간복잡도: 평균적으로 O(nlogn)으로 매우 빠른 속도를 보임
추가적인 메모리 공간을 거의 사용하지 않는 in-place정렬
최악의 경우에는 성능이 O(N^2)까지 내려감.
비교횟수
첫번째 호출에서 N개의 요소가 피벗과 비교됨
두번째 호출에서 N/2 *2로 N번 비교, 세번째도 N회 비교함.
배열이 균형있게 나뉜다면(절반에 가깝게) O(nlogn)이 걸리지만 배열이 이미 정렬되어 있는 상태라면 O(N^2)
Merge Sort
분할정복 방식을 사용하는 정렬방법.
1.
배열을 반으로 나눈다
2.
왼쪽 하위 배열에 대한 병합정렬을 재귀호출함
3.
오른쪽 하위 배열에 대한 정렬을 재귀호출함
4.
정렬된 두 하위 배열을 하나의 정렬된 배열로 병합: 임시 배열을 통해 병합된 요소를 저장함. 각 하위 배열의 요소를 비교하고 임시배열에 정렬된 순서로 저장함. 이후 임시배열의 내용을 원래 배열에 복사.
배열을 반으로 나누는 과정은 최대 logN번 발생함.
각 병합 단계에서는 O(N)시간이 소요됨. 모든 요소를 비교하고 복사하는 과정이 포함되기 때문.
전체 시간복잡도는 O(nlogn)이며 안정 정렬임
#include <iostream>
using namespace std;
// Merge 함수: 두 개의 정렬된 부분 배열을 병합
template <class ItemType>
void Merge(ItemType values[], int leftFirst, int leftLast, int rightFirst, int rightLast) {
int tempSize = rightLast - leftFirst + 1;
ItemType* tempArray = new ItemType[tempSize]; // 임시 배열
int index = 0;
int saveFirst = leftFirst; // 첫 번째 위치 저장
while (leftFirst <= leftLast && rightFirst <= rightLast) {
if (values[leftFirst] <= values[rightFirst]) {
tempArray[index++] = values[leftFirst++];
} else {
tempArray[index++] = values[rightFirst++];
}
}
// 왼쪽 부분 배열의 남은 값 복사
while (leftFirst <= leftLast) {
tempArray[index++] = values[leftFirst++];
}
// 오른쪽 부분 배열의 남은 값 복사
while (rightFirst <= rightLast) {
tempArray[index++] = values[rightFirst++];
}
// tempArray의 값을 원래 배열로 복사
for (index = 0; index < tempSize; index++) {
values[saveFirst + index] = tempArray[index];
}
delete[] tempArray; // 임시 배열 메모리 해제
}
// MergeSort 함수: 재귀적으로 정렬 수행
template <class ItemType>
void MergeSort(ItemType values[], int first, int last) {
if (first < last) {
int middle = (first + last) / 2;
MergeSort(values, first, middle); // 왼쪽 부분 배열 정렬
MergeSort(values, middle + 1, last); // 오른쪽 부분 배열 정렬
Merge(values, first, middle, middle + 1, last); // 병합
}
}
int main() {
int arr[] = {38, 27, 43, 3, 9, 82, 10};
int size = sizeof(arr) / sizeof(arr[0]);
cout << "Before sorting: ";
for (int i = 0; i < size; i++) {
cout << arr[i] << " ";
}
cout << endl;
MergeSort(arr, 0, size - 1);
cout << "After sorting: ";
for (int i = 0; i < size; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
C++
복사
성능비교
Testing
정렬 알고리즘을 테스트하기 위해서 다양한 크기의 배열을 사용해서 성능을 측정하고 역순 정렬, 거의 정렬된 배열, 동일한 요소로 구성된 배열 등에 대해 성능을 평가한다.
객체를 정렬할때는 객체에 대한 참조를 조작하는 것이다.
Stable Sort
안정정렬은 중복 요소의 순서를 유지하는 정렬 방법으로 quick sort와 heap sort는 불안정이다. 병합정렬과 삽입정렬은 안정정렬이다.
검색 알고리즘
1.
선형검색: 리스트의 첫번째 요소부터 시작해서 원하는 요소를 찾기 위해 각 요소의 키를 검사한다. 간단하지만 비효율적일 수 있다.
2.
고확률 순서: 가장 자주 찾는 요소를 리스트의 앞부분에 배치해서 검색 효율성을 높인다.
3.
High-Probablitiy list: 검색된 요소를 리스트의 앞부분으로 이동시켜 이후 검색 시 빠르게 접근할 수 있게 함
4.
Key ordering: 요소가 존재하지 않은 경우 리스트를 모두 검사하기 전에 검색을 중단해 불필요한 작업을 줄임
Binary Search
이진탐색은 정렬된 배열에서 특정 요소를 찾는 검색 알고리즘이다. 배열을 반으로 나누어가며 검색을 진행한다
1.
정렬된 배열 = info, 찾는 요소 = item, 검색 범위를 정의하는 fromLoc과 toLoc을 입력함
2.
배열의 첫번째 인덱스가 마지막 인덱스보다 클 경우 검색하고자 하는 요소가 배열에 존재하지 않음
3.
현재 검색 범위의 중간 인덱스 mid를 계산함 (fromLoc + toLoc) / 2
4.
info[mid]가 item과 같으면 해당 요소를 찾은것이니 true
item이 더 작으면 검색범위를 왼쪽 하위 배열로 줄여서 재귀적으로 이진탐색
item이 더 크면 검색범위를 오른쪽 하위 배열로 줄여서 재귀적으로 이진탐색
template<class ItemType>
bool BinarySearch(ItemType info[], ItemType item, int fromLoc, int toLoc) {
// Pre: info[fromLoc .. toLoc] sorted in ascending order
// Post: Function value = (item in info[fromLoc .. toLoc])
int mid;
if (fromLoc > toLoc) // base case -- not found
return false;
else {
mid = (fromLoc + toLoc) / 2;
if (info[mid] == item)
return true; // base case -- found at mid
else if (item < info[mid]) // search lower half
return BinarySearch(info, item, fromLoc, mid - 1);
else // search upper half
return BinarySearch(info, item, mid + 1, toLoc);
}
}
C++
복사
정렬된 배열에서만 사용할 수 있으며 시간복잡도는 O(logN)으로 우수함
Hashing
해싱은 리스트의 요소를 빠르게 정렬하고 접근할 수 있는 방법. O(1)의 시간 복잡도로 요소를 검색할 수 있다.
키 값의 해시함수를 사용해서 리스트 내의 위치를 식별한다. 해시함수는 주어진 키값을 해시테이블의 인덱스로 변환한다.
예를들어 회사에서 제작한 부품 번호가 4자리인 경우
Hash(Key) = partNum mod 100
Hash(5502) = 2
하지만 두개 이상의 키가 동일한 해시 위치를 생성하는 상황에서는 충돌이 일어난다
Resolving Collision
선형 탐색
해시함수로 생성된 위치에서 시작해서 빈 위치를 찾을때까지 인덱스를 순차적으로 증가시킨다.
HashValue + 1 % 100
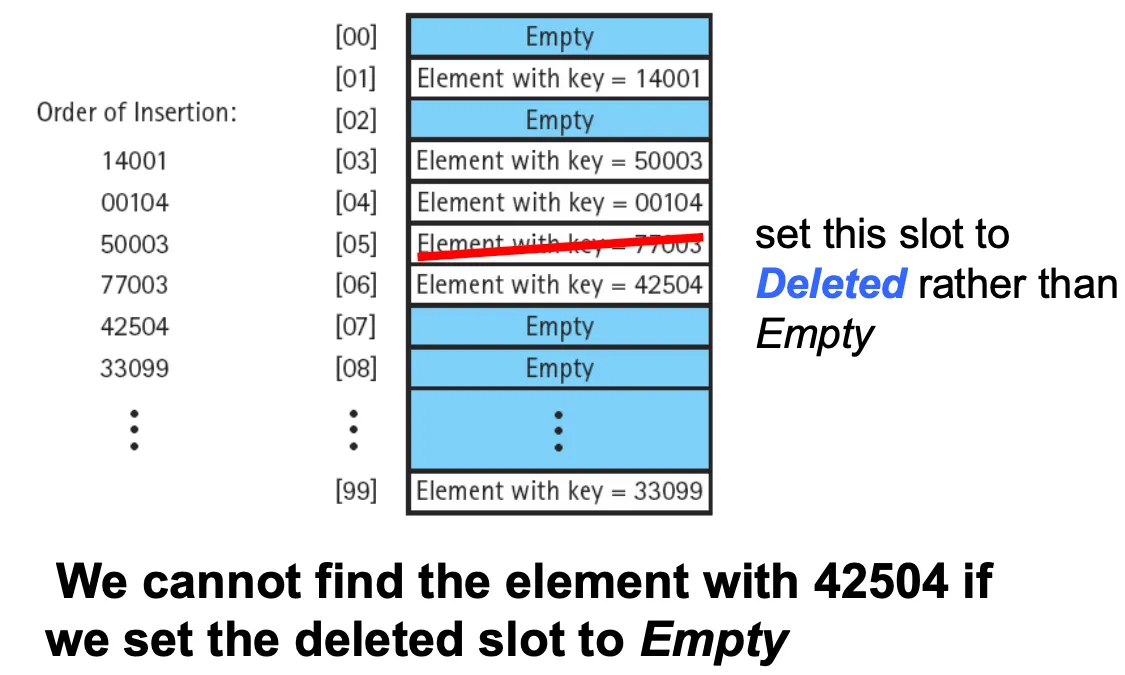
선형탐색을 사용해서 요소를 삭제할때는 슬롯을 empty말고 deleted로 표시한다. 해당 위치가 여전히 충돌을 해결하는데 사용될 수 있기 때문이다.
Rehasing
충돌이 발생했을때 새로운 해시 위치를 계산함. (선형탐색도 포함됨)
Quadratic Probing: 인덱스를 제곱한 값을 더해서 새로운 위치를 계산
Random probing: 무작위 수를 추가해서 새로운 해시 위치를 계산함
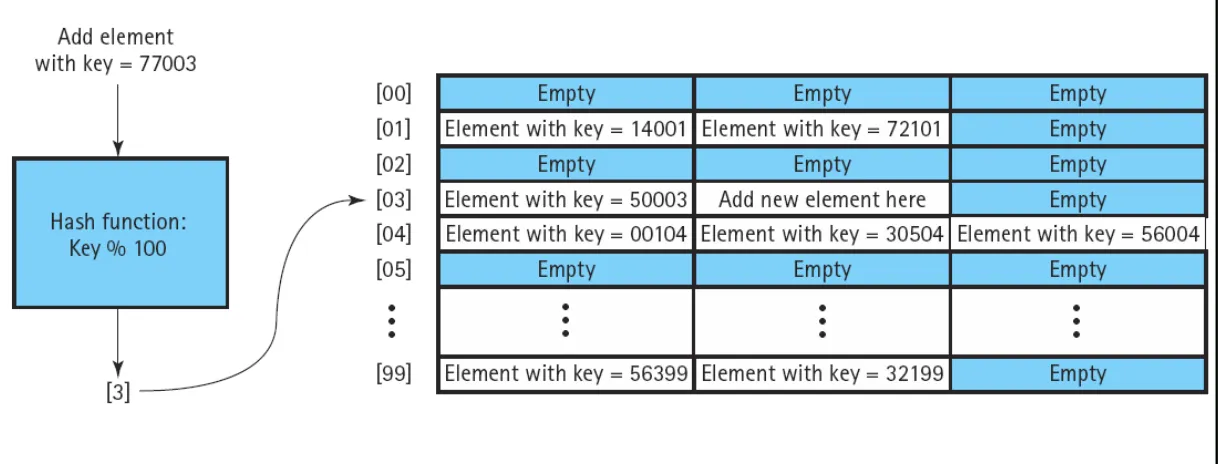
Bucket and Chaining
동일한 해시를 가진 키를 같은 위치에 여러개 저장할 수 있도록 함
•
Bucket: 특정 해시 위치에 연관된 요소들의 집합. 각 버킷은 여러 요소를 포함할 수 있음
•
Chain: 동일한 해시 위치에 있는 요소들을 연결 리스트 형태로 저장함. 충돌이 발생해도 원래의 해시 위치에 여러 요소를 쉽게 저장할 수 있음.
Collision을 최소화하기 위한 방법
•
해시 테이블의 크기를 늘리거나
•
더 넓은 범위의 해시값을 생성하는 해시함수를 사용하는것.
•
해시 테이블 내에서 요소들이 균일하게 분포되도록 한다
좋은 해시함수 선택
•
키의 통계적 분포 활용: 입력 데이터의 분포를 이해하고 이에 맞는 해시함수 선택
Radix Sort
기수정렬은 숫자의 각 자리수를 기준으로 정렬하는 방법. 정수나 문자열을 정렬하는데 사용됨.
1.
가장 낮은 자리수부터 시작해서 가장 높은 자리수까지 정렬한다.
2.
각 자리수에 대해 0부터 9까지 큐를 사용해서 해당 자리수의 값에 따라 레코드를 분배함
3.
각 자리수를 정렬할때는 안정 정렬 알고리즘을 사용해서 같은 값의 원소들이 원래 순서 유지
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
// 가장 큰 숫자의 자리수를 찾는 함수
int getMax(const std::vector<int>& arr) {
return *std::max_element(arr.begin(), arr.end());
}
void countingSort(std::vector<int>& arr, int exp) {
int n = arr.size();
std::vector<int> output(n); // 정렬된 결과를 저장할 배열
int count[10] = {0}; // 각 자리수의 개수를 세기 위한 배열
// 해당 자리수의 개수 세기
for (int i = 0; i < n; i++) {
count[(arr[i] / exp) % 10]++;
}
// 누적 개수 계산
for (int i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
// 정렬된 배열 생성
for (int i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// 정렬된 결과를 원래 배열에 복사
for (int i = 0; i < n; i++) {
arr[i] = output[i];
}
}
// 기수 정렬 함수
void radixSort(std::vector<int>& arr) {
int maxNum = getMax(arr); // 배열에서 가장 큰 숫자 찾기
// 각 자리수에 대해 Counting Sort 수행
for (int exp = 1; maxNum / exp > 0; exp *= 10) {
countingSort(arr, exp);
}
}
int main() {
std::vector<int> arr = {170, 45, 75, 90, 802, 24, 2, 66};
radixSort(arr);
std::cout << "정렬된 배열: ";
for (int num : arr) {
std::cout << num << " ";
}
return 0;
}
C++
복사
기수정렬은 비교를 사용하지 않으므로 O(N*k)의 시간복잡도를 가짐
안정정렬이며 추가적인 메모리를 필요로 한다.
정수나 문자열을 정렬할때 매우 효율적이다.