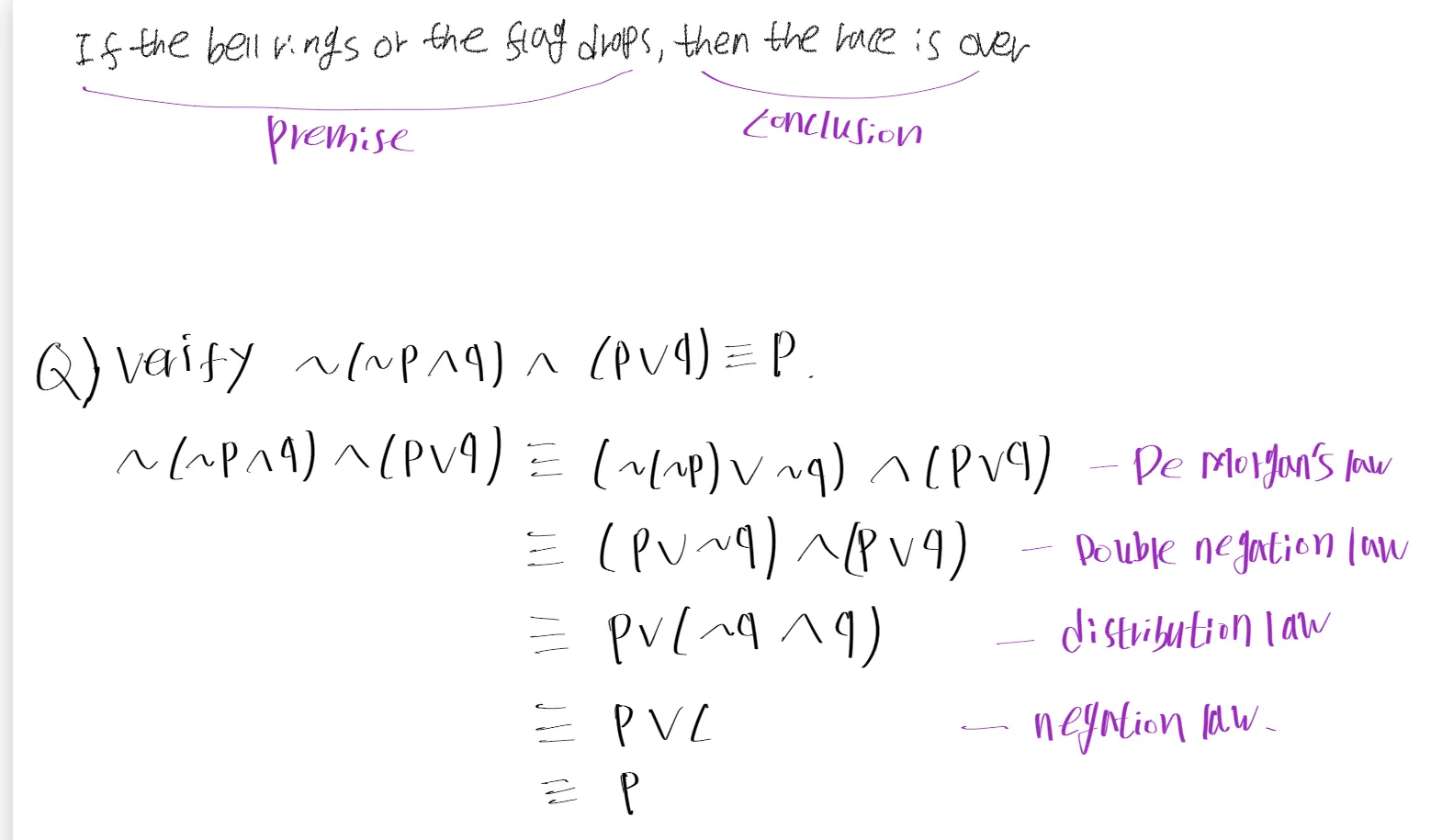Logical From and Logical Equivalence
Statement
A statement is a sentence that is true or false but not both.
참 혹은 거짓으로 나타낼 수 있지만 둘 다는 아닌 문장.
statement를 표현하기 위해서 statement variable을 사용함. ex) p→q
Statement인것
•
”Bob has a tennis racket”
•
2+2=4
Statement가 아닌것
•
x = 10
•
I am heavy
Componund statements
compound statements = statements + logical operators
Logical operators
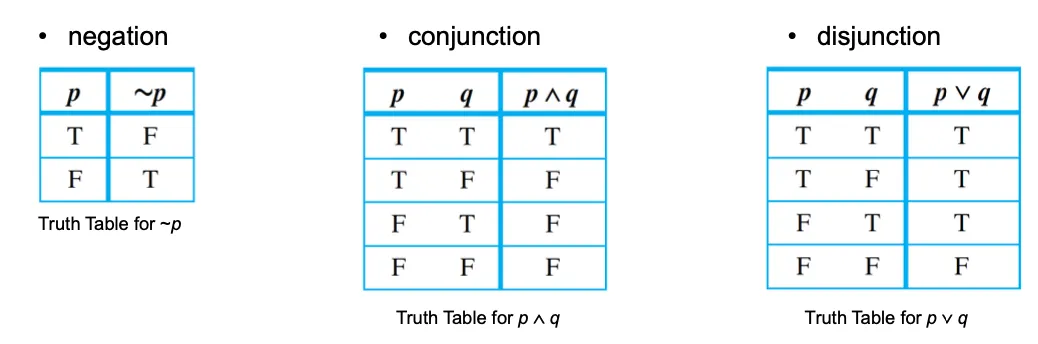
•
~p = negation of p
•
p∧q = conjunction of p and q
•
p∨q = disjunction of p and q
negation이 가장 먼저 수행된다.
Statement Forms
statement variable과 logical connective(~, ∧, ∨)로 구성된 statement
p but q = p and q
neither p nor q = ~p and ~q
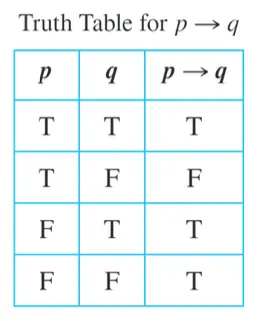
Truth Table
statement의 statement variable들에 대해 가능한 모든 truth value의 조합을 나타내는 표.
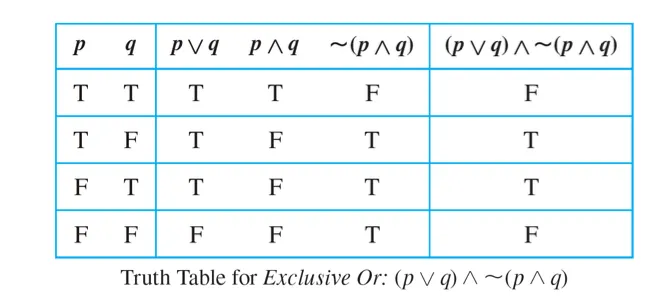
exclusive or(XOR) = (p∨q) ∧ !(p∧q)
다르면 true가 된다.
Argument
Assertion의 truth를 증명하기 위한 연속된 statements
assertion의 끝부분을 conclusion이라고 하고 이전의 statement를 premise라고 함.
Argument Form
sequence of statement forms.
If Socrates is a man, then Socrates is mortal.
Socrates is a man.
∴ Socrates is mortal.
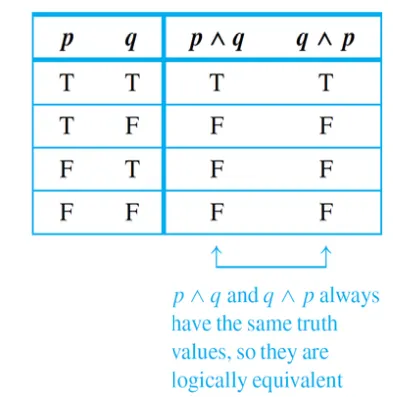
Logical Equivalence
두 개의 statement form이 logically equivalent하면 동일한 truth table값을 가진다. P ≡ Q
∼(∼p) ≡ p
De Morgan’s Laws
and statement의 negation은 각 요소의 negation의 or statement와 같다
or statement의 negation은 각 요소의 negation의 and statement와 같다.
Tautology (t)
무조건 참인 statement ex) p ∨ ~p, ~(~p) ≡ p
p∧ t ≡ p.
Contradiction (c)
무조건 거짓인 statement. ex) p∧~p
p∧c ≡ c.
Conditional Statements
If p then q, p implies q, p → q
p: hypothesis, q: conclusion
ex) If 4686 is divisible by 6, then 4686 is divisible by 3
p의 truth에 따라서 q의 truth가 결정되기 때문에 conditional하다고 부른다.
p가 true인데 q가 false인 경우에만 statement가 false
Q) If 0 = 1 then 1 = 2. True or False?
A)hypothesis가 false이므로 statement는 true이다.
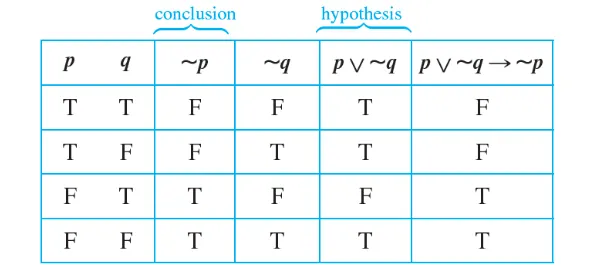
Q) p ∨ ~q → ~p의 truth table은?
Negation of conditional statement
~ (p → q) ≡ p ∧ ~q
~ (p → q) ≡ ~(~p ∨ q) ⇒ De Morgan’s law
≡ ~(~p) ∧ (~q)
≡ p ∧ ~q
Contrapositive (대우명제)
p → q의 대우명제는 ~q → ~p.
conditional statement는 자신의 대우명제와 logically equivalent.
Converse and inverse (역과 이)
If p then q
converse: if q then p
inverse: if ~p then ~q
converse와 inverse는 원래 statement와 logically equivalent하지 않다.
converse와 inverse는 대우관계이다.
Only if
p only if q means that p can take place only if q takes place also.
≡ if q does not take place, then p cannot take place
≡ if ~q, then ~p
≡ if p then q
Biconditional
“p if, and only if, q”
"p iff q”
p  q : true if p and q have the same truth values, false if p and q have opposite truth values
q : true if p and q have the same truth values, false if p and q have opposite truth values
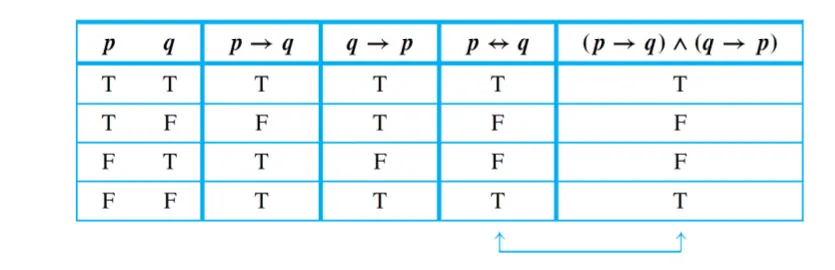
p  q ≡ (p → q) ∧(q → p)
q ≡ (p → q) ∧(q → p)
Logical Operator 순서
Necessary, Sufficient conditions
necessary condition = 필요조건.
r is a necessary conditionfor s = r이 일어나지 않으면 s는 일어날 수 없다.
sufficient condition = 충분조건.
r is a sufficient condition for s = r이 일어나면 s가 일어나는것이 보장된다.
ex) If John is eligible to vote, then he is at least 18 years old.
투표할 수 있다는 것은 18살을 넘었다는 것의 충분조건.
18살을 넘었다는 것은 투표할 수 있다는 것의 필요조건.
Valid and Invalid Arguments
If Socrates is a man, then Socrates is mortal.
Socrates is a man.
∴ Socrates is mortal.
이 Argument form을 abstraction하면
If p then q (p → q)
p
∴ q
argument form이 valid하다는것은 premise가 모두 참일 때 conclusion이 참이라는 것을 뜻한다.
논증이 정당하고 전제가 참일 때 결론의 참은 전제의 참으로부터 추론되었다고 한다.
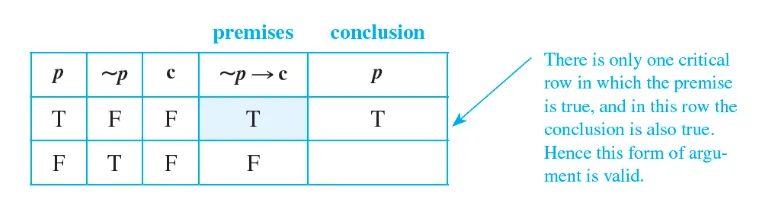
truth table에서 모든 전제가 참인 row를 critical row라고 한다.
critical row에서 conclusion이 false인 경우가 존재한다면 그 argument form은 invalid하다
모든 critical row에서 conclusion이 true이면 그 argument form은 valid하다.
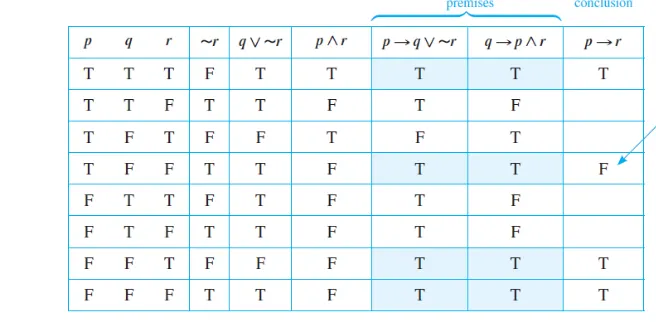
Q) 이 Argument form이 valid한지 결정하라
p → q ∨ ∼r
q → p ∧ r
∴ p → r
전제가 모두 참인 critical row에서 conclusion이 false인 경우가 있으므로 invalid
Modus ponens & modus tollens
two premises(대전제와 소전제) and one conclusion = syllogism(삼단논법)
modus ponens(긍정논법)
If p then q
p
∴ q
modus tollens(부정논법)
If p then q
~q
∴~p
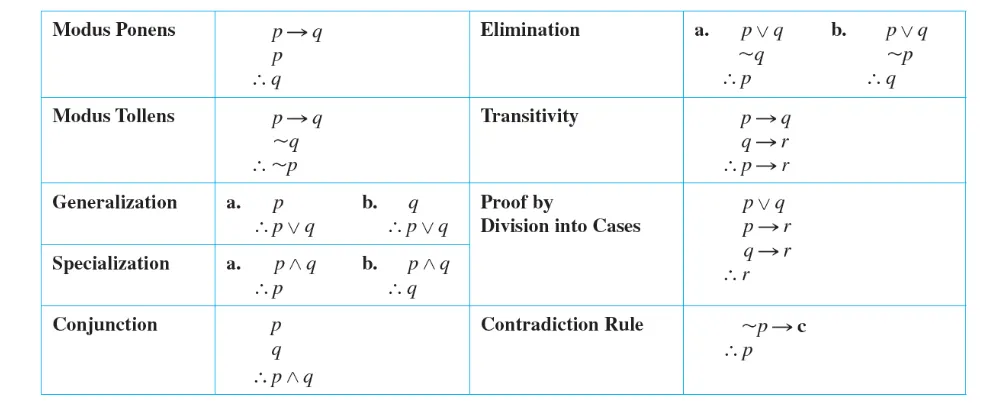
Rules of inference
연역추론에 쓰이는 방법들
•
Generalization
ex) p, ∴ p ∨ q
q가 어떤것이든 상관없이 더 general하므로 항상 참이다.
•
Specialization
ex) p ∧ q, ∴p
•
Elimination
두가지 가능성 중 하나를 제외하고 남는것이 참이다.
•
Transitivity
p→q, q→r, ∴p→r
•
Proof by division into cases
p ∨ q
p → r, q → r
∴ r
Fallacies
converse Error(역오류) = 결과긍정오류
p → q
q
∴ p
Inverse Error(이오류) = 전제부정오류
p → q
∼p
∴ ∼q
Validity ≠ truth
논증이 정당하다고 해서 결론이 반드시 참이라고 할수는 없다.
논증이 정당하다는 것은 전제가 모두 참일 때 결론이 참이 되는것을 보장하는것이지,
전제가 거짓인 경우에 대해서도 보장하는것은 아니다.
또한 논증이 부당하다고 해서 결론이 반드시 거짓인것은 아니다.
부당한 논증은 전제가 모두 참일 경우에도 결론이 거짓인 경우가 존재할 수 있다는 것이다.
argument가 valid하고 전제가 참일때 sound(완전)하다고 하며 그렇지 않은 경우 unsound(불완전)
Contradiction rule
명제 p가 거짓이라고 가정했을 때 논리적으로 모순이 되면 p가 참이라고 결론을 내린다.
Q) argument가 valid한지 보여라.
~p → c, where c is a contradiction
∴ p
Summary
Predicates and Quantified Statements
Prediates
술어 = 유한개의 변수를 가지고 있으며 특정 값을 대입하면 명제가 되는 문장.
한 개의 변수를 갖는 술어의 변수에 해당 정의역의 값을 대입하면 그 결과명제는 참 혹은 거짓이 된다.
predicate을 true로 만드는 element들의 set을 truth set이라고 한다.
ex) Predicate Q(n) = “n is a factor of 8”. Find the thruth set of Q(n) if the domain of n is Z.
(Z = integer)
A) {1, 2, 4, 8, -1, -2, -4, -8}
Quantified Statements
술어 P(x)의 술어변수 x에 대해 적절한 한정을 추가하여 술어 P(x)가 명제가 되도록 할 수 있는데, 이러한 명제를 한정화 명제라고 한다.
Quantifier
•
universal quantifier: ∀
for every, for each, for all 등으로 읽는다.
Every human being is mortal = ∀ human beings x, x is mortal,
H가 human being의 set일때, ∀x ∈ H, x is mortal.
•
Existential Quantifier: ∃
there exists, there is a, for at least one 등으로 읽는다.
There is a student in Math 140 = ∃ a person p such that p is a student in Math 140
P가 학생들의 set일때, ∃ p ∈ P such that p is a student in Math 140
Informal language
Formal한 방식은 프로그램으로 옮길 때 편리하지만 복잡하고 직관적으로 이해하기 힘들다.
Universal conditional statement (전칭조건명제)
∀x, if P(x) then Q(x).
ex)∀x ∈ R, if x > 2 then x2 > 4.
∀x ∈ D, Q(x)는 ∀x, if x is in D then Q(x)로도 쓸수 있다
“∃x such that P(x) and Q(x).”
→ “∃x ∈ D such that Q(x)”, where D is the set of all x for which P(x) is true.”
Bound variables and Scope
•
(1) For every integer x, x2 ≥ 0
•
(2) There exists a real number x such that x3 = 8
두가지 statement에서 쓰인 x는 다른 의미를 가지며 변수는 quantifier에 bound되어서 그 scope를 벗어나면 의미를 가지지 않는다.
Implicit Quantification
If a number is an integer, then it is a rational number.
all, every등의 단어를 포함하지 않아도 articla a로 인해서 묵시적으로 universal quantification의 의미를 포함한다. ex) If x > 2 then x² > 4 ⇒∀ real numbers x, if x > 2 then x2 > 4.
double arrow로 implicit quantification을 표현할 수 있다
P(x)와 Q(x)를 술어라 하고 D를 x의 정의역이라 할 때,
•
표기 P(x) ⇒ Q(x) 는 P(x) 의 진리집합이 Q(x) 의 진리집합에 포함된다는 뜻임: ∀x, P(x) → Q(x).
•
표기 P(x) ⇔ Q(x) 는 P(x) 와 Q(x) 의 진리집합이 동일하다는 뜻임: ∀x, P(x)  Q(x).
Q(x).
Negation of universal Statements
universal statement의 negation은 existential statement와 동일하다. 역도 성립한다.
all are → some are not
~(∀x, P(x) → Q(x)) ≡ ∃x such that ~(P(x) → Q(x))
ex) ∀ primes p, p is odd.
negation ⇒ ∃ a prime p such that p is not odd.
Relation with De Morgan’s law
universal statement는 and statement와 동일하고
existential statement는 or statement와 동일하다.
•
∃x ∈ D such that Q(x) ≡ Q(x1) ∨ Q(x2) ∨ … ∨ Q(xn)
•
∀x ∈ D, Q(x) ≡ Q(x1) ∧ Q(x2) ∧ … ∧ Q(xn)
universal conditional statement도 자신의 대우명제와 logically equivalent
∀x ∈ D, if P(x) then Q(x) ≡ ∀x ∈ D, if ~Q(x) then ~ if P(x)
Statements with multiple Quantifiers
∀∃ statement (universal existential statement)
A statement containing both ∀ and ∃, where the ∀ comes before the ∃:
∀x in set D, ∃y in set E such that x and y satisfy property P(x, y).
universal existential statement의 truth를 증명하려면 D에서 어떤 요소 x를 뽑던지 E에 y를 만족하는 요소가 하나라도 있어야 한다.
∃∀ statement (existential universal statement)
A statement containing both ∀ and ∃, where the ∃ comes before the ∀:
∃ an x in D such that ∀y in E, x and y satisfy property P(x, y).
existential universal statement는 E에서 어떤 요소 y를 뽑더라도 x를 만족하는 요소가 D에 있어야 한다.
quantifier의 순서가 변경되면 의미가 완전히 달라진다.
ex) Tarski world
Q)There is a triangle x such that for every circle y, x is to the right of y.
A)Either d or i would work for all of the three circles, a, b, and c
Negation of statements with more than one Quantifier
•
∼(∀x in D, ∃y in E such that P(x, y)) ≡ ∃x in D such that ∼(∃y in E such that P(x, y))
≡ ∃x in D such that ∀y in E,∼P(x, y).
•
∼(∃x in D such that ∀y in E, P(x, y)) ≡ ∀x in D, ∼(∀y in E, P(x, y))
≡ ∀x in D, ∃y in E such that ∼P(x, y).
Arguments with Quantified Statements
universal instantiaition
어떤 set에 대해서 모든 property가 true이면, 특정 하나의 property도 true이다.
universal instantiation은 연역 추론의 기본적인 도구이다.
All men are mortal.
Socrates is a man.
∴ Socrates is mortal.
Universal modus ponens & modus tollens
If an integer is even, then its square is even.
k is a particular integer that is even.
∴ k2 is even
All human beings are mortal.
Zeus is not mortal.
∴ Zeus is not human.
Using a Diagram to Show Validity
All human beings are mortal.
Felix is mortal.
∴ Felix is a human being.
conclusion이 반드시 premise로부터 도출되는것이 아니므로 invalid하다
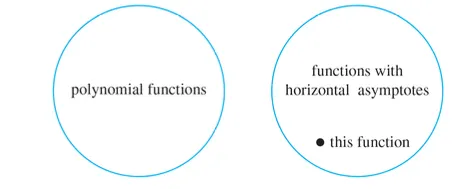
No polynomial functions have horizontal asymptotes.
This function has a horizontal asymptote.
∴ This function is not a polynomial function.