Relations
Objects of mathematics may be related in various ways.
xample:
A set A may be said to be related to a set B if
•
A is a subset of B
•
A is not a subset of B
•
A and B have at least one element in common
A number x may be said to be related to y if
•
x < y
•
x is a factor of y
•
x2 + y2 = 1
x is related to y = x R y
Let A = {0, 1, 2} and B = {1, 2, 3}
A × B = {(a, b) ∣ a ∈ A and b ∈ B} = {(0, 1),(0, 2),(0, 3),(1, 1),(1,2 ),(1, 3),(2, 1),(2, 2),(2, 3)}
관계 = 주어진 조건에 의해 관계가 있는 원소들의 순서쌍 모두의 집합.
Example: let's say we have two sets A = {1, 2, 3} and B = {4, 5, 6, 7} and a relation R⊆A×B as:
R={(1, 5),(2, 6),(3, 5)}
•
B = {4, 5, 6, 7} →co-domain, {5, 6} → image (range)
Domain: 정의역, Co-domain: 공변역(치역과 다름), image=range: 치역
A가 정의역이고 B가 공변역이 된다.
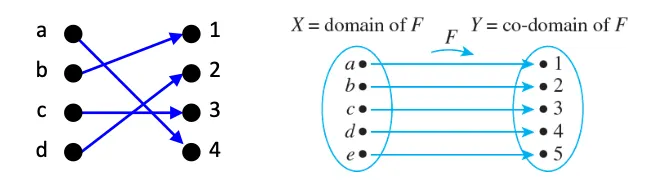
Arrow diagram of a relation
Draw an arrow from x to y
if, and only if, x R y
if, and only if, (x, y) ∈ R.
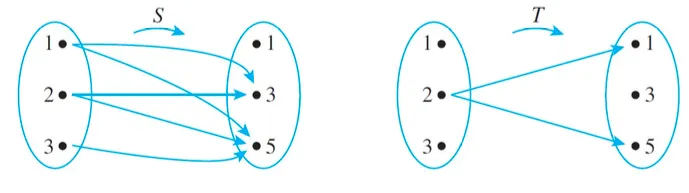
Q. Let A = {1, 2, 3} and B = {1, 2, 3} and define relations S and T from A to B as follows:
For every (x, y) ∈ A × B, (x, y) ∈ S means that x < y, T = {(2, 1), (2, 5)}.
Relation에서 한 원소는 다른 방향으로 여러개의 화살표를 가질 수 있고 화살표가 출발하지 않는 원소도 있음.
Function as a relation
Relation F from A to B가 함수일 조건
1.
모든 A의 원소 x에 대해 (x,y) ∈ F인 B의 원소 y가 존재
2.
F에 있는 서로 다른 두 순서쌍은 다른 첫번째 원소를 갖는다.
만일 A와 B가 집합이고, F가 A로부터 B로의 함수이면, A에 있는 임의의 원소 x에 대하여, F에 의해 x와
관계가 있는 B의 유일한 원소를 F(x)로 표기하고, ‘F of x’ 라고 읽는다.
f(x) = f of x, 입력 x에 대한 f의 출력, f에 의한 x의 상
preimage: 원상, inverse image: 역상
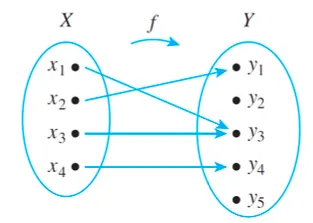
1. Every element of X has an arrow that points to an element in Y.
2. No element of X has two arrows that point to two different elements of Y.
Functions defined by formulas
A function f from X to Y, denoted f : X → Y is an assignment of each element of A
to exactly one element of B.
We write f(a) = b if b is the unique element of B assigned by the function f to the element a of A.
Functions acting on sets
집합 X에서 집합 Y로의 함수가 주어지면, X의 부분집합의 모든 원소들의 Y로의 상의 집합과, Y의 부분집합의 모든 원소들의 X로의 역상의 집합을 고려할 수 있다.
Equality of functions
F: X →Y 와 G: X → Y 가 함수이면, 모든 ∈ X에 대하여 F(x) = G(x) 일 경우에만 F = G 이다
A function is a special kind of relation and a relation is a subset of a Cartesian product.
Example of functions
Identity function (항등함수)
정의역과 공역이 같고, 모든 원소를 자기 자신으로 대응시키는 함수.
Whatever is input to the identity function comes out unchanged.
Hamming Distance function
The Hamming distance function gives a measure of the “difference” between two strings of 0’s and 1’s that have the same length. Let Sn be the set of all strings of 0’s and 1’s of length n.
H: Sn × Sn → Z(nonneg)
H(s, t) = the number of positions in which s and t have different values.
n = 5, H(11111, 00000) = 5, whereas H(11000, 00000) = 2
길이가 같은 두 문자열의 차이의 척도. 다른 문자의 개수
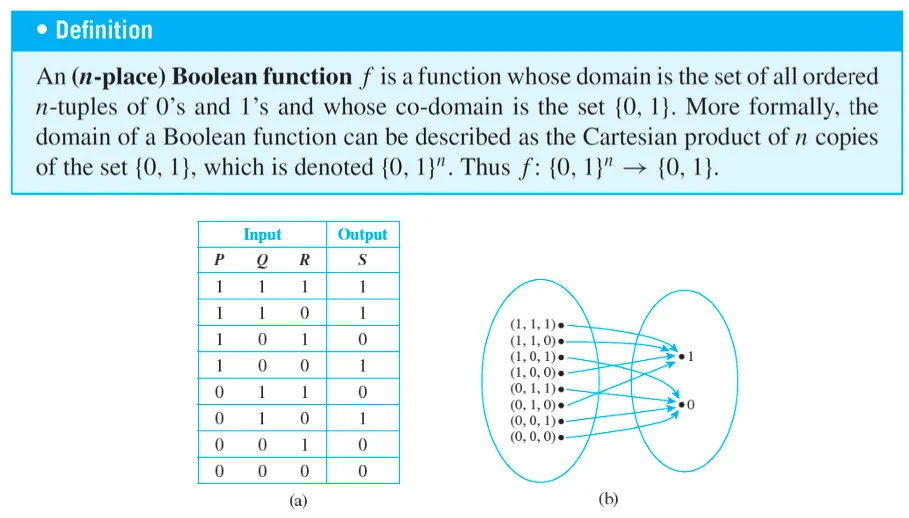
Boolean Function
One-to-one, Onto, Inverse Functions
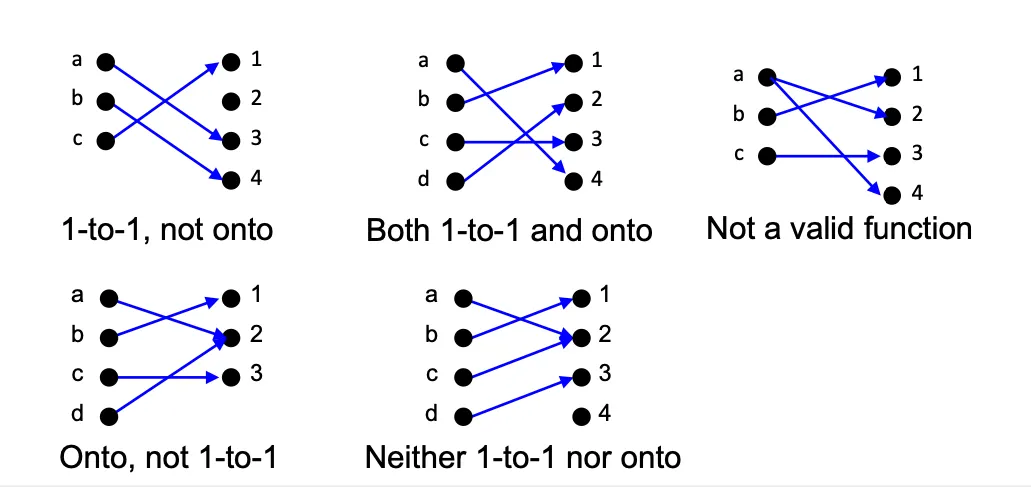
one-to-one or injective (단사, 일대일)
no two arrows that start in the domain point to the same element of the co-domain
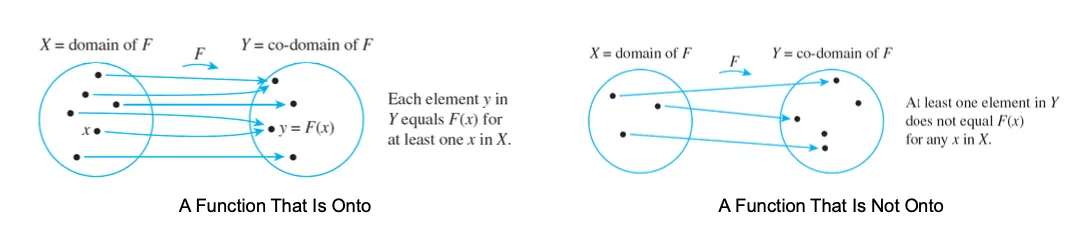
onto or surjective (전사, 전사상)
– every element of a function’s co-domain may be the image of some element of its domain.
– When a function is onto, its range is equal to its co-domain.
one-to-one correspondences (일대일 대응)
단사함수이면서 전사함수인 함수는 일대일 대응. 일대일 대응이면 정의역과 공변역이 완벽하게 match되고 co-domain으로부터의 inverse function을 정의할 수 있다.
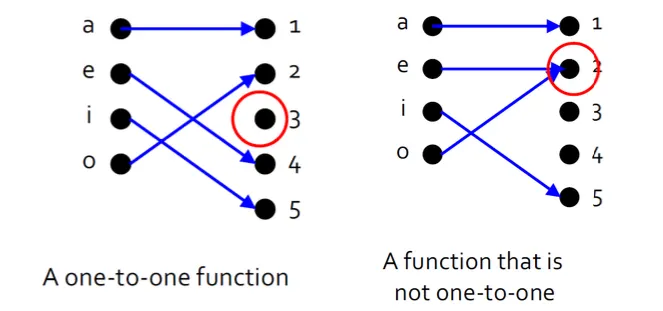
One-to-one functions
Arrow diagram에서, 2개 이상의 정의역 원소들이 같은 공변역 원소에 대응될 수 있다.
하지만 정의역의 2개의 화살표가 공변역에서 같은 원소에 대응되지 않으면, 그러한 함수를 일대일 또는 단사
라고 부른다.
One-to-one functions on infinite sets
f is one-to-one if, and only if, the following universal statement is true:
∀x1, x2 ∈ X, if f(x1) = f(x2) then x1 = x2.
f가 단사함수라는것을 증명하기 위해서 direct proof를 사용한다.
suppose x1 and x2 are elements of X such that f(x1) = f(x2) and show that x1 = x2.
disprove를 위해서: find elements x1 and x2 in X so that f(x1) = f(x2) but x1 ≠ x2.
Q. Define f : R → R and g : Z → Z by the rules
f(x) = 4x − 1 for all x ∈ R and g(n) = n2 for all n ∈ Z
a. Is f one-to-one? Prove or give a counterexample.
b. Is g one-to-one? Prove or give a counterexample.
a. To prove, we need to prove that
∀ real numbers x1 and x2, if f(x1) = f(x2) then x1 = x2.
Proof: Suppose x1 and x2 are real numbers such that f(x1) = f(x2). [We must show that x1 = x2.]
By definition of f, 4x1 − 1 = 4x2 − 1. This gives 4x1 = 4x2, x1 = x2 [as was to be shown].
b. Counterexample: Let n1 = 2 and n2 = − 2.
Then by definition of g, g(n1) = g(2) = 2^2 = 4 and also g(n2) = g(−2) = (−2)^2 = 4
Hence, g(n1) = g(n2), but n1 ≠ n2, and so g is not one-to-one.
Hash Functions
Transform input data of any size into a fixed-size output
•
Quick data access and retrieval
•
Widely used in cryptography, data structures, cashes and databases, etc.
Example
•
Suppose we create a table for KHU students, each with a student ID number.
•
Naïve method: place the record with ID number n (e.g. 2022109999) at the nth position
– Student number has 10 digits, so this requires a table with 9,999,999,999 positions
– What if we have no more than 100 students? Do we really need this huge table?
– This would waste computer memory space
Alternative method: Suppose there are only 5 students, and define a function Hash, from the set of student ID numbers to the set {0, 1, 2, 3, …, 9, 10} as follows:
Hash (n) = n mod 11 for each ID number n
Two input values may collide (have the same output value)
•
When the collision occurs, apply one of the collision resolution methods
•
One of the simplest – a linear probe(선형탐사)
해시 함수를 통해 해시 값을 계산합니다.
해당 해시 값의 위치에 이미 값이 존재하는지 확인합니다.
만약 해당 위치가 비어 있지 않다면, 다음 위치로 이동하여 비어 있는 첫 번째 위치를 찾습니다.
비어 있는 위치를 찾으면 그곳에 ID 번호를 저장합니다.
데이터를 효율적으로 저장하기 위해서 해시함수는 단사함수여야하며 공변역이 10억보다 작아야 한다.
대부분의 해시함수는 mod연산을 사용하고 소수를 사용해서 값이 분산되어있도록 한다.
또한 공변역을 정의역보다 50~100% 더 크게 만든다.
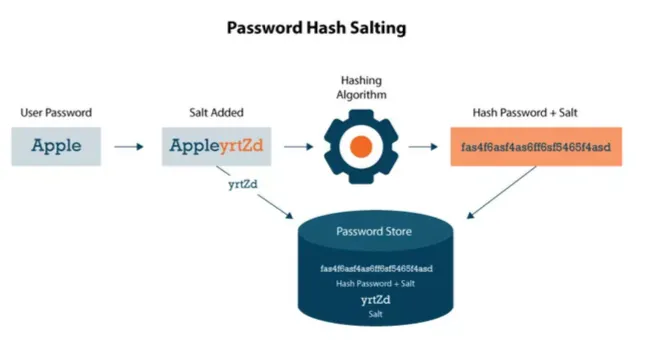
Cryptographic Hash function
고정길이 비트 문자열을 출력하며, 충돌이 일어날 가능성이 매우 작아야 하며 해시값에서 원래 데이터를 찾을 수 없어야 한다. 또한 대량의 데이터에 대해 빠르게 계산하고 입력의 작은 변화에도 출력 문자열의 변화가 커야 한다
⇒ avalanche effect
비밀번호를 salt와 함께 hashing 알고리즘을 통해 해싱하고 그것을 서버에 저장한다.
파일자체를 해싱해서 내용이 변경되거나 에러가 발생했는지를 체크해서 데이터의 무결성을 보장할 수 있다.
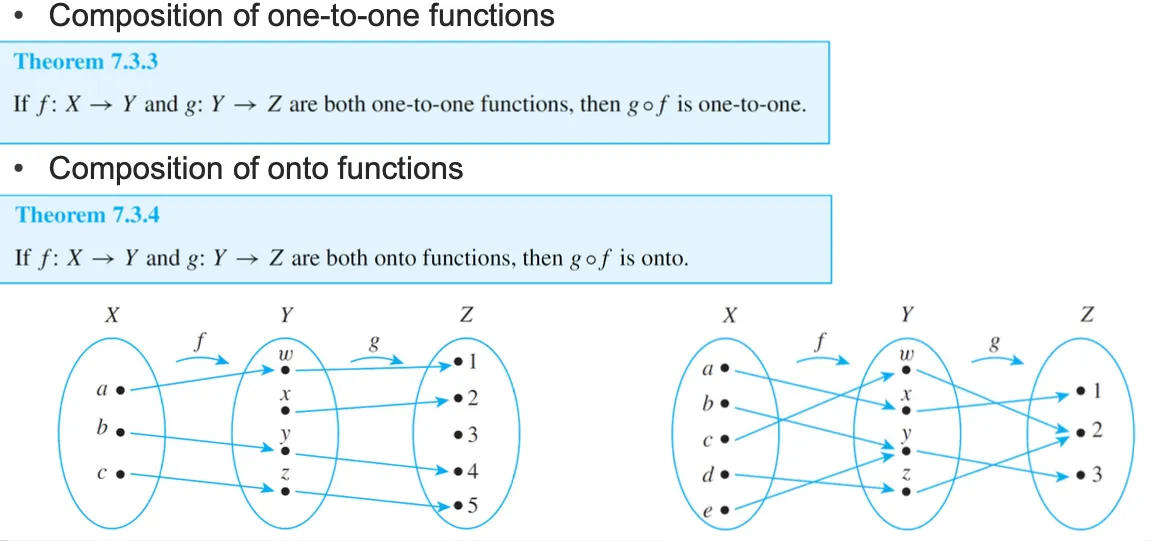
Onto Functions
every element in a function’s co-domain to be the image of some element in its domain,
such a function is called onto (전사) or surjective (전사상).
(함수 공변역의 모든 원소가 해당 정의역의 어떤 원소의 image 이다)
Proving or Disproving That Functions are Onto
∀y ∈ Y, ∃x ∈ X such that F(x) = y.
Thus to prove F is onto, you will ordinarily use the method of generalizing from the generic particular:
suppose that y is any element of Y and show that there is an element x in X with F(x) = y.
To disprove (show that f is not onto), find an element y of Y such that y ≠ F(x) for any x in X.
One-to-one Correspondence
F: X→Y가 one-to-one 이면서 onto인것.
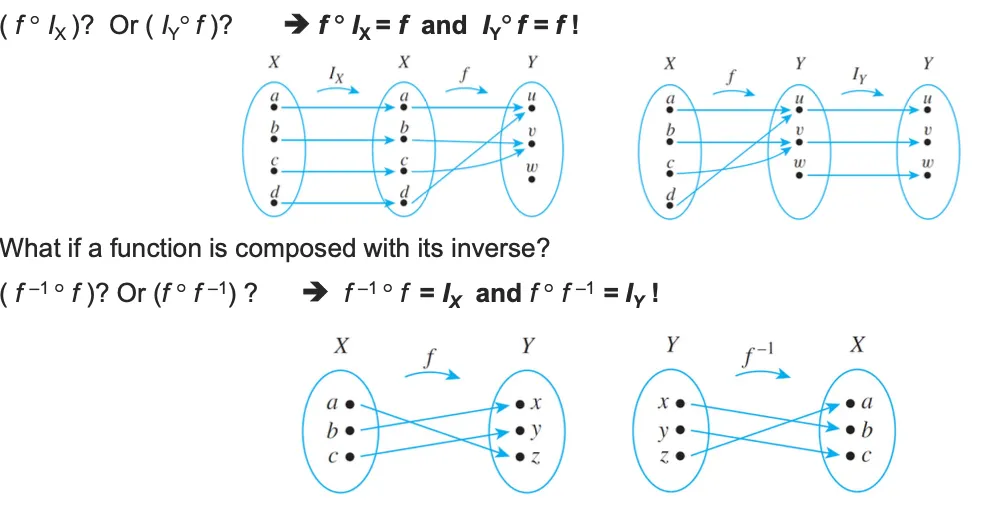
Inverse Function
Let f is a bijection from X to Y.
Then the inverse of f (inverse function for f, 역함수), denoted f –1, is the function from Y to X defined as f –1(y) = x iff. f(x) = y
역삼수는 전단사 함수에서만 존재할 수 있다.
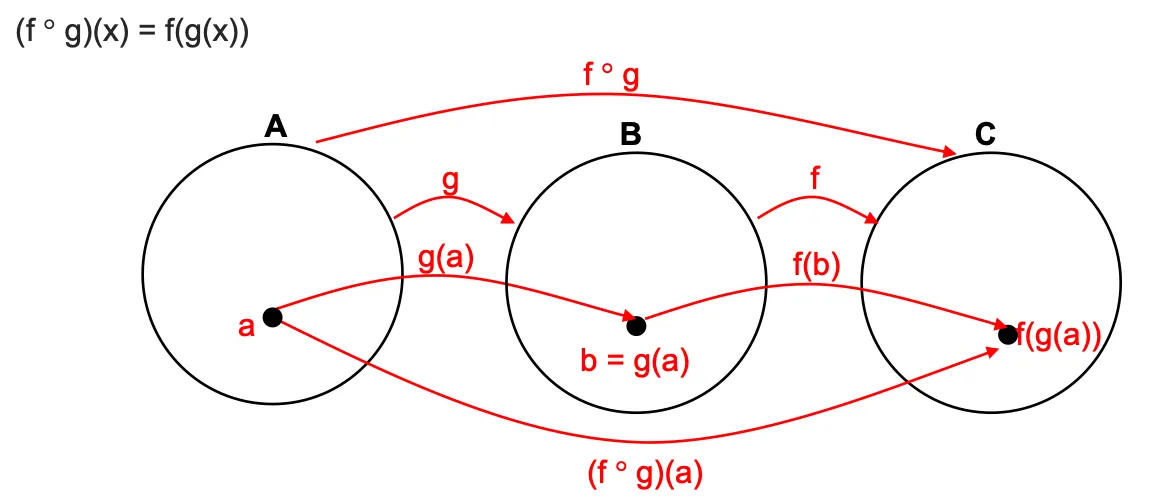
Compositions of functions
f(g(x)) ≠ g(f(x))
The composition (합성) can be formed only if the output of the first function is acceptable input to the second function. (첫 번째 함수의 출력 값이 두 번째 함수의 입력 값으로 받아들일 수 있을 때)
The range of the first function must be contained in the domain of the second function.
(즉, 첫 번째 함수의 치역이 두 번째 함수의 정의역에 포함되어야 한다)
What is the inverse of f ° g ? → (f ° g)–1 = g–1 ° f–1