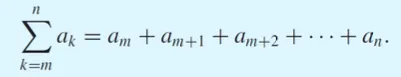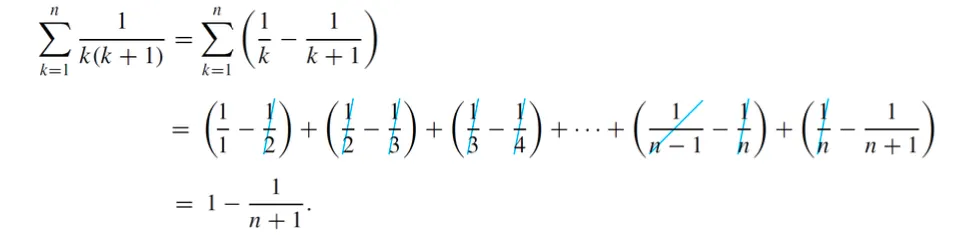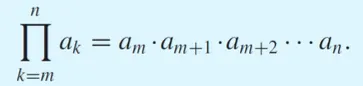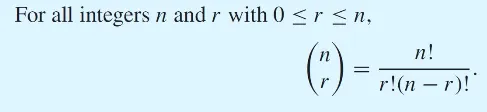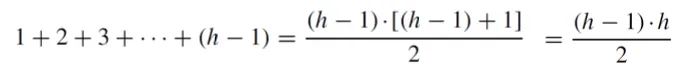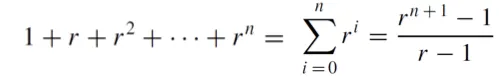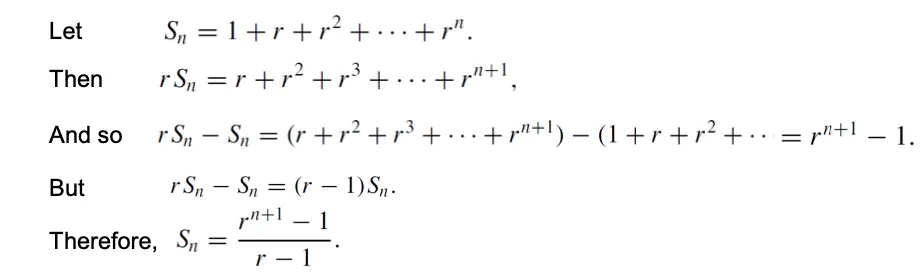Sequences
A sequence is a function whose domain is either all the integers between two given integers or all the integers greater than or equal to a given integer.
am, am + 1, am + 2, … , an,
ak (read “a sub k”) is called a term.
k in ak is called a subscript or index
am, am + 1, am + 2, … = infinite sequence
k = m에서 k=n까지의 summation의 표현
Successive Cancellation of terms
Product Notation
pi 기호를 사용해서 m부터 n까지의 곱을 표현한다.
Factorial
n factorial denoted n! is defined to be the product of all the integers from 1 to n
n! = n(n-1)…*3*2*1
Zero factorial 0! = 1
n coose r notation
nCr, C(n,r) 등으로 표기
C = combination. number of subsets of size r that can be chosen from a set with n elements.
Mathematics Inductions
수학적 귀납법
P(n)이 증명해야 할 statement일때,
Step1 basic step ⇒ P(a)가 true임을 보인다.
Step2 inductive step ⇒ 모든 integers k≥a 에 대해 P(k)가 true라고 가정했을때 P(k+1)이 true임을 보인다.
closed form
특정 숫자들의 합이 공식과 같다고 보이는 것(생략부호)
For an integer h ≥ 2, write 1 + 2 + 3 + ... + (h − 1) in closed form.
Geometric sequence(등비수열)
각 항이 이전 항에 상수를 곱한 값인 항을 등비수열이라고 한다.
The sum of the first n terms of this sequence is given by the formula
for every integer n ≥ 0 and every real number r not equal to 1.
Proof.
Defining sequences
첫번째 방법은 첫번째 몇개의 항을 나열하는 방법(informal)
두번째 방법은 nth term을 explicit formula로 나타내는 방법
세번째 방법은 점화식을 사용하는 방법.
recurrence relation(점화식)은 이전항을 통해서 다음항을 나타내는 방정식. 한개이상의 initial value도 포함.
For every integer k ≥ 2, ck = ck − 1 + kck − 2 + 1
c0 = 1 and c1 = 2
c2, c3, c4를 찾아라
c2 = c1 + 2c0 + 1 by substituting k = 2 into (1)
= 2 + 2 · 1 + 1 since c1 = 2 and c0 = 1 by (2)
∴ c2 = 5
c3 = c2 + 3c1 + 1 by substituting k = 3 into (1)
= 5 + 3 · 2 + 1 since c2 = 5 by (3) and c1 = 2 by (2)
∴ c3 = 12
c4 = c3 + 4c2 + 1 by substituting k = 4 into (1)
= 12 + 4 · 5 + 1 since c3 = 12 by (4) and c2 = 5 by (3)
∴ c4 = 33
Recursion (재귀)
•
To find a way to break it down into smaller subproblems each having the same form as the
original problem
•
and to do this in such a way that when the process is repeated many times, the last of the
subproblems are small and easy to solve and the solutions of the subproblems can be woven
together to form a solution to the original problem.
ex) Tree, Divide and Conquer, Backtracking Algorithms..
ex) 피보나치 수열
올해의 시작에 암수 한쌍의 토끼가 태어났다. 토끼들은 첫번째 달 동안에는 새끼를 낳을 수 없고 다로 다음 달부터 암수 한쌍의 새끼를 매달 낳는다. 토끼들이 죽지 않는다고 가정했을 때, 올해 끝에는 몇마리의 토끼가 있을까?
month k에 태어나는 토끼쌍의 수는 month k-2에 존재하는 토끼쌍의 수와 같다.
month k의 토끼쌍의 수는 그 달에 태어나는 토끼의 수 + 이전 달의 토끼의 수와 같으므로 Fk = Fk-1 + Fk-2이다
(3) F2 = F1 + F0 = 1 + 1 = 2 by (1) and (2)
(4) F3 = F2 + F1 = 2 + 1 = 3 by (1), (2), and (3)
(5) F4 = F3 + F2 = 3 + 2 = 5 by (1), (3), and (4)
(6) F5 = F4 + F3 = 5 + 3 = 8 by (1), (4), and (5)
(7) F6 = F5 + F4 = 8 + 5 = 13 by (1), (5), and (6)
(8) F7 = F6 + F5 = 13 + 8 = 21 by (1), (6), and (7)
(9) F8 = F7 + F6 = 21 + 13 = 34 by (1), (7), and (8)
(10) F9 = F8 + F7 = 34 + 21 = 55 by (1), (8), and (9)
(11) F10 = F9 + F8 = 55 + 34 = 89 by (1), (9), and (10)
(12) F11 = F10 + F9 = 89 + 55 = 144 by (1), (10), and (11)
(13) F12 = F11 + F10 = 144 + 89 = 233 by (1), (11), and (12)
따라서 233쌍 = 466마리가 된다.
Iteration
다음 항이 이전 항에 상수를 더한 값인 수열을 등차수열(arithmetic sequence)라고 한다.
ak = ak-1 + d for all integers k≥1
an = a0 + dn for all integers n≥0
다음 항이 이전 항에 상수를 곱한 값인 수열을 등비수열(geometric sequence)라고 한다.