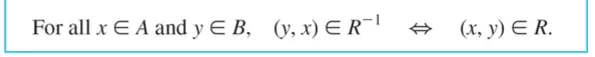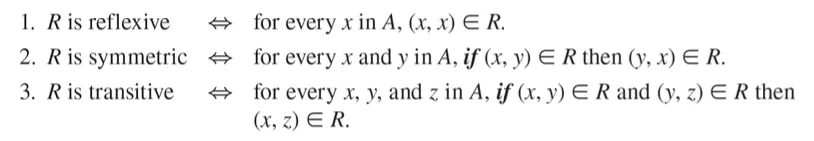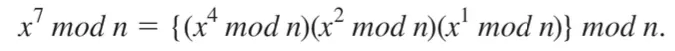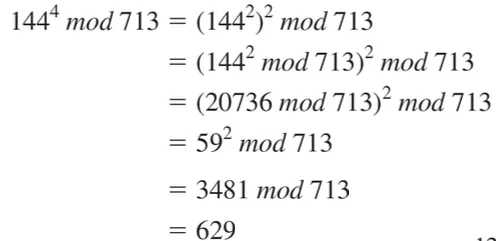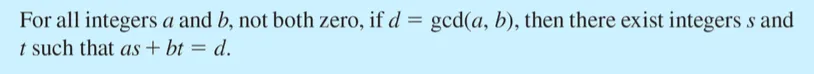The inverse of relation
Relation R –1 from B to A can be defined
•
By interchanging the elements of all the ordered pairs of R.
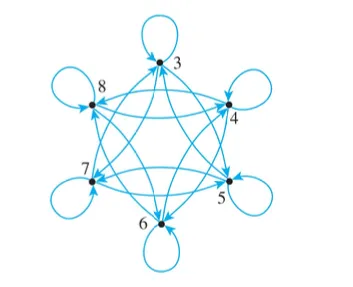
Let A = {2, 3, 4} and B = {2, 6, 8}, and let R be the “divides” relation from A to B:
For every ordered pair (x, y) ∈ A × B, x R y ⇔ x | y.
Ordered pairs in R and R –1?
•
R = {(2, 2), (2, 6), (2, 8), (3, 6), (4, 8)}, R –1 = {(2, 2), (6, 2), (8, 2), (6, 3), (8, 4)}
R –1 in words?
•
y R–1x ⇔ y is a multiple of x.
Directed graph of a relation
Directed graph
– Draw an arrow from each point of A to each related point.
– If a point is related to itself, a loop is drawn that extends out from the point and goes back to it.
N-ary relations
•
ordered pair E.g. (x1, x2)
•
It’s also a 2–tuple
•
Thus, we call it as a binary relation (*bi-nary)
– A subset of a Cartesian product of two sets
What about relations with n-tuple?
•
n-ary relations
– n-ary relation is a subset of a Cartesian product of n sets.
Reflexivity, symmetry, and transitivity
1. Reflexive (반사적이다): Each element is related to itself
– 모든 x ∈ A 에 대하여 x R x 인 경우
2. Symmetric (대칭적이다): If any one element is related to any other element, then the second element is related to the first.
– 모든 x, y ∈ A 에 대하여 x R y 이면 y R x 인 경우
3. Transitive (추이적이다): If any one element is related to a second and that second element is related to a third, then the first element is related to the third.
– 모든 x, y, z ∈ A 에 대하여 x R y 이고 y R z 이면 x R z 인 경우
The relation induced by a partition
분할은 합집합이 A이며 공통원소를 갖지 않으면서 공집합이 아닌 집합들의 모음.
집합 A의 partition이 주어졌을때 유도되는 관계: x와 y가 동시에 속하는 부분집합 Ai가 존재한다
Partition of A: {0, 3, 4}, {1}, {2}.
Since {0, 3, 4} is a subset of the partition,
0 R 3 because both 0 and 3 are in {0, 3, 4}, 0 R 4 because both 0 and 4 are in {0, 3, 4}, 3 R 4 because both 3 and 4 are in {0, 3, 4}, Also, 0 R 0 because both 0 and 0 are in {0, 3, 4}
3 R 3 because both 3 and 3 are in {0, 3, 4},
4 R 4 because both 4 and 4 are in {0, 3, 4}.
Since {1} is a subset of the partition, and since {2} is a subset of the partition, 3 R 0 because both 3 and 0 are in {0, 3, 4},
4 R 0 because both 4 and 0 are in {0, 3, 4},
4 R 3 because both 4 and 3 are in {0, 3, 4}.
1 R 1 because both 1 and 1 are in {1},
2 R 2 because both 2 and 2 are in {2}.
Hence R = {(0, 0), (0, 3), (0, 4), (1, 1), (2, 2), (3, 0), (3, 3), (3, 4), (4, 0), (4, 3), (4, 4)}.
partition에서 유도된 relation은 reflexivity, symmetry, transitivity를 다 만족한다.
Equivalence relation
A relation on a set that satisfies the three properties of reflexivity, symmetry, and transitivity is
called an equivalence relation (동치 관계).
•
세 개의 성질을 만족시키는 집합에서의 관계
herefore, “the relation induced by a partition” is an equivalence relation
Equivalence classes of an equivalence relation
원소 a 와 relation R 관계가 있는 모든 원소들의 부분집합
(Lemma 1) If two elements of A are related by an equivalence relation R, then their equivalence classes are the same.
Proof? Show [a] ⊆ [b] and [b] ⊆ [a].
Proof that [a] ⊆ [b]: Let x ∈ [a]. [We must show that x ∈ [b].]
Since x ∈ [a], then x R a. Also, a R b by hypothesis.
Lastly, as R is an equivalence relation, by transitivity, x R b. Hence x ∈ [b]
Proof that [b] ⊆ [a]: Let x ∈ [b]. [We must show that x ∈ [a].]
Since x ∈ [b], then x R b. Also, a R b by hypothesis, and b R a by symmetry.
Lastly, by transitivity, x R a. Hence x ∈ [a]
(Lemma 2) any two equivalence classes of an equivalence relation are
either mutually disjoint or identical.
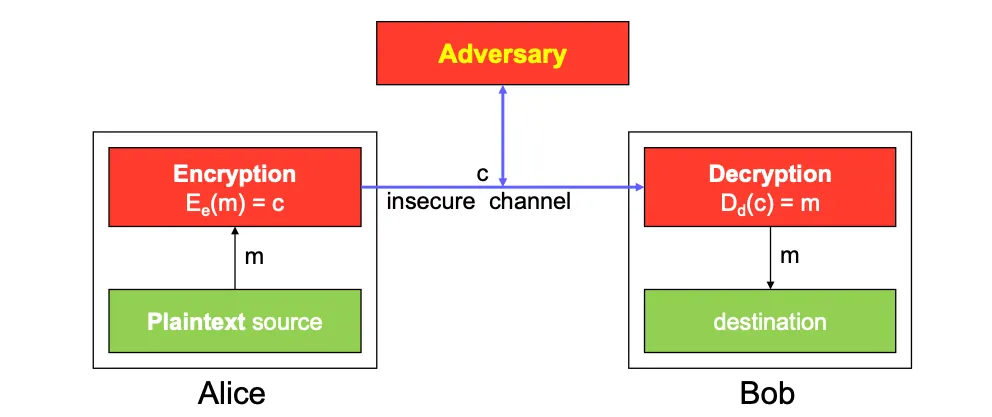
Cryptograph
m: plaintext (평문), c: ciphertext (암호문)
Caesar cipher
Julius Caesar created secret messages by shifting each letter three letters forward in the alphabet (sending the last three letters to the first three letters.)
For example, the letter B is replaced by E, X to A, Y to B, and the letter Z is replaced by C.
This process of making a message secret is an example of encryption.
f(p) = (p + 3) mod 26
recover = decryption할때는 f(p) = (p - 3) mod 26
f(p) = (p + k) mod 26에서 k는 key이다.
Affine ciphers
Shift ciphers are a special case of affine ciphers which use functions of the form
f(p) = (ap + b) mod 26, a and b are integers, chosen so that f is a bijection.
The function is a bijection if and only if gcd(a,26) = 1
cryptanalysis: 암호해독. 암호화 방식과 키에 대한 정보 없이 암호문에서 평문을 복원하는 과정
An important tool for cryptanalyzing ciphertext produced with a affine ciphers is the relative frequencies of letters.
The nine most common letters in the English texts are
• E 13%, T 9%, A 8%, O 8%, I 7%, N 7%, S 7%, H 6%, and R 6%.
Block ciphers
Example: Using the transposition cipher based on the permutation σ of the set {1,2,3,4} with
σ(1) = 3, σ(2) = 1, σ(3) = 4, σ(4) = 2,
a. Encrypt the plaintext PIRATE ATTACK
Solution:
a. Split into four blocks PIRA TEAT TACK.
Apply the permutation σ giving IAPR ETTA AKTC.
Cryptosystems
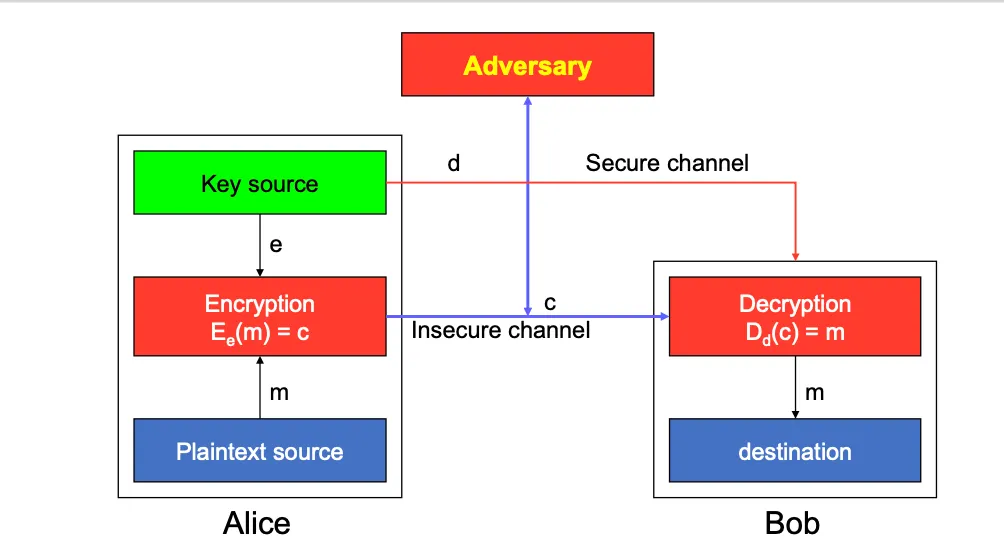
Definition: A cryptosystem is a five-tuple (P,C,K,E,D), where
•
P is the set of plaintext strings (평문),
•
C is the set of ciphertext strings (암호문),
•
K is the keyspace (set of all possible keys),
•
E is the set of encryption functions, and
•
D is the set of decryption functions.
Dk(Ek(p)) = p, for all plaintext strings p.
Symmetric-key encryption
If an encryption scheme is based on symmetric-key (대칭키)
•
Then for each (Ek, Dk) it is computationally easy to compute Ek knowing Dk and Dk knowing Ek
•
Usually Ek = Dk
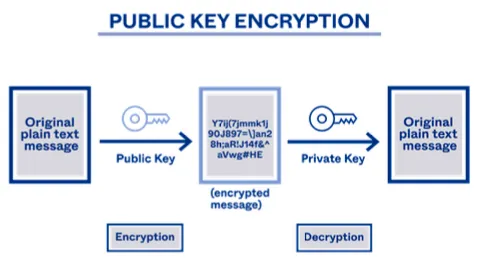
Public-key encryption
Every entity has a private key SK (비밀키) and a public key PK (공개키)
•
Public key is known to all
•
It is computationally infeasible to find SK from PK
•
Only SK can decrypt a message encrypted by PK
SSH, HTTPS, 이메일 암호화 등에 적용된다.
RSA (Rivest–Shamir–Adleman) Asymmetric cryptography (비대칭암호화)
Based on function that is hard to invert (one-way function)
– 즉, 입력을 출력으로 계산은 쉽지만, 출력을 보고 입력을 알아내는 것은 매우 힘듦
Use the practical difficulty of factoring the product of two large prime numbers
Properties of congruence modulo n
Modulo n, or quotient-remainder theorem (a = nq + r, 0 ≤ r < n) indicates that there are exactly n possible remainders that can occur. (Modulo n에서 발생할 수 있는 나머지의 수가 정확히 n개이다)
Modular Arithmetic
For a given integer, these two gives the same result.
Perform addition, subtraction, or multiplication on integers and then reduce the result modulo n
Reduce the integers modulo n, perform addition, subtraction, or multiplication, and reduce the result modulo n
For example,
•
(5 · 8) = 40 ≡ 1 (mod 3)
•
(5 mod 3) (8 mod 3) = 2 · 2 = 4 ≡ 1 (mod 3).
Q. The most practical use of modular arithmetic is to reduce computations involving large integers to computations
involving smaller ones. (큰 수에 대한 계산을 작은 수에 대한 계산으로 간단하게 만드는..)
•
For instance, note that 55 ≡ 3 (mod 4) because 55 − 3 = 52, which is divisible by 4, and 26 ≡ 2 (mod 4)
because 26 − 2 = 24, which is also divisible by 4.
Verify the following statements.
a. 55 + 26 ≡ (3 + 2) (mod 4) b. 55 − 26 ≡ (3 − 2) (mod 4)
c. 55 · 26 ≡ (3 · 2) (mod 4) d. 552 ≡ 32 (mod 4)
Answer.
a. b. c. d. 55 + 26 = 81 and 3 + 2 = 5. To show that 81 ≡ 5 (mod 4), we need to show that
4 | (81 – 5). True.
55 − 26 = 29 and 3 − 2 = 1. To show that 29 ≡ 1 (mod 4), we need to show that 4 | (29 – 1). True.
55 · 26 = 1430 and 3 · 2 = 6. … we need to show that 4 | (1430 – 6). True.
55 · 55 = 3025 and 3 · 3 = 9. … we need to show that 4 | (3025 – 9). True.
When modular arithmetic is performed with very large numbers, as is the case for RSA crytography, computations are facilitated by using two properties of exponents.
Q. Find 1444 mod 713
Euclidean algorithm (유클리드 호제법)
Efficient way to compute the greatest common divisor of two integers
gcd(a, b): 최대공약수, gcd(r, 0) = r
A = Bq + r 에서, C를 A와 B의 공약수로 두자. 그러면 , A = NC, B = MC로 둘수있고,
치환하면 NC = (MC)q + r 이된다. 이를 r에 대해 풀면 r = C (N – MQ)가 된다.
즉 , 모든 A와 B의 공약수 C는 r과 b의 공약수이다. 즉gcd(A, B) ≤ gcd (B, r)이다.
D를 B, r의 공약수로 놓는 방법으로 gcd (B, r) ≤ gcd(A, B)를 증명할 수 있다.
그러므로 gcd(A, B) = gcd (B, r)이다.
정수 a, b에 대해 as + bt = d 를 만족시키는 정수 s와 t가 존재할 때, d를 a와 b의 선형결합이라고 함.
Inverse modulo n
Suppose we want to find x for 2x ≡ 3 (mod 5).
We can first find x that makes 2x ≡ 1 (mod 5) → 2 · 3 ≡ 1 (mod 5) (Inverse of modulo n),
and then multiply it by 3 → 2 · 3 · 3 ≡ 3 (mod 5).
Thus, x ≡ 4 (mod 5)
Relatively prime (서로소) → inverse modulo n exists
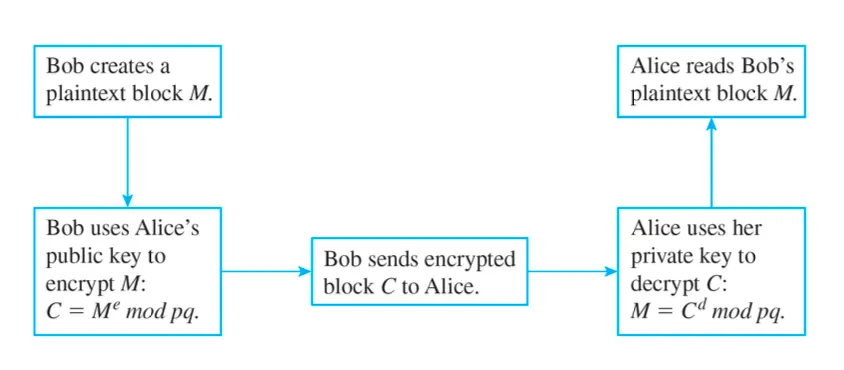
RSA cryptography
Public key, private key를 만들기 위해서, 큰 random prime p, q 를 고른다 (비슷한 크기의).
그리고 n = pq, 그리고 1 < e < (p– 1)(q– 1) 이며 gcd((p– 1)(q– 1), e) = 1 인 정수 e 를 선정
Public key: (n, e)
Encryption (암호화): c ≡ m^e mod n 이 공개키로 보낼 메시지를 암호화 가능
개별 prime number p, q 는 공개하지 않으며, 이를 이용해 메시지 복호화
Private key: d, from ed ≡ 1 mod (p-1)(q-1)
Inverse modulo 를 계산하는 것과, n = pq 를 인수 분해하는 것은 계산 복잡도가 동등
Decryption (복호화): m ≡ c^d mod n