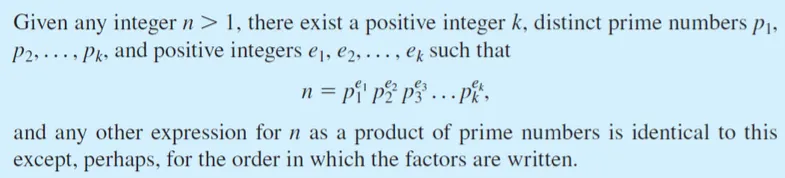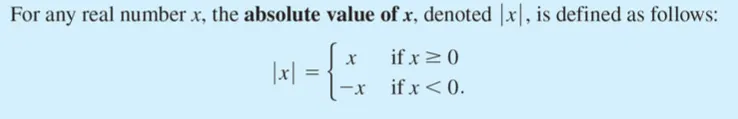Direct Proof and Counterexample
Even and Odd
n is even ⇒ n = 2k for some integer k
n is odd ⇒ n = 2k+1 for some integer k
a. Is 0 even?
Yes, 0 = 2·0.
b. Is −301 odd?
Yes, –301 = 2(–151) + 1.
c. If a and b are integers, is 6a2b even?
6a2b = 2(3a2b), and since a and b are integers, so is 3a2b
Prime and composite integers (소수와 합성수)
prime = if and only if n > 1 and for all positive integers r and s, if n = rs, then either r or s equals n.
composite = if and only if n > 1 and n=rs for some integer r and s with 1 < r < n and 1< s < n
prime은 n=rs이면 모든 양의 정수 r과 s에 대해서 하나는 1이고 하나는 n인 수이다.
composite은 n=rs일때 적어도 하나의 양의 정수 쌍 r과 s에 대해서 둘다 1보다 크고 n보다 작은 수
a. Is 1 prime?
No. A prime number is required to be greater than 1.
b. Is every integer greater than 1 either prime or composite?
b. Yes. Let n be any integer that is greater than 1. Consider all pairs of positive integers r and s such that n = rs.
•
There exist at least two such pairs, namely, r = n and s = 1 and r = 1 and s = n. Moreover, since n = rs, all such pairs satisfy the inequalities 1 ≤ r ≤ n and 1 ≤ s ≤ n.
•
If n is prime, then these two pairs are the only ways to write n as rs.
•
Otherwise, there exists a pair of positive integers r and s such that n = rs and neither r nor s equals either 1 or n.
Therefore, in this case 1 < r < n and 1 < s < n, and hence n is composite.
Proving universal Statements
∀x ∈ D, if P(x) then Q(x)에서 D가 유한한 집합이고 P(x)를 만족시키는 요소가 유한할때,
method of exhaustion을 사용해서 증명할 수 있다. (해당하는 경우 모두 나열)
∀n ∈ Z, if n is even and 4 ≤ n ≤ 26 then n can be written as a sum of two prime numbers.
4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, 10 = 5 + 5
12 = 5 + 7, 14 = 11 + 3, 16 = 5 + 11, 18 = 7 + 11
20 = 7 + 13, 22 = 5 + 17, 24 = 5 + 19, 26 = 7 + 19
method of generalizing from the generic particular(일반화법)
모든 x가 특정 조건을 만족시킨다고 증명하기 위해서는 임의의 x를 뽑아서 만족시킴을 보인다.
method of direct proof (직접증명법)
“If P(x) then Q(x),”를 증명하기 위해서 x를 임의로 D에서 뽑고 P(x)가 true임을 보인다.
정의를 이용해서 Q(x)도 true임을 보인다.
the sum of any two even integers is even.
∀ integers m and n, if m and n are even them m + n is even
Suppose m and n are [particular but arbitrarily chosen] even integers.
By the definition of even, m = 2r and n = 2s for some integer r and s
Then,
m + n = 2r + 2s ··· by substitution
= 2(r + s) ··· by factoring out a 2.
Let t = r + s. Note that t is an integer because it is a sum of integers. Hence
m + n = 2t where t is an integer
It follows by the definition of even that m + n is even.
Disproving universal statements by counterexample
P(x)가 true이지만 Q(x)가 false인 값 x를 찾는다. (반례)
ex)∀ real numbers a and b, if a² = b² then a = b
0.5, -0.5는 real number이고 a² = b²이지만 a = b는 성립하지 않는다. Q.E.D
Proving Existential Statements
∃x ∈ D such that Q(x)를 증명하기 위해서 D에서 Q(x)를 만족하는 x를 하나 찾으면 된다. = 구성적 존재증명
비구성적 존재증명 = Q(x)를 true로 만드는 x의 존재가 공리나 증명된 이론으로부터 보장되는 것을 보이거나 만족하는 x가 없으면 contradiction이 일어난다는 것을 보임
existential statement가 false이려면 universal statement가 true여야 한다.
There is a positive integer n such that n² + 3n + 2 is prime
Negation: For all positive integers n, n² + 3n + 2 is not prime
n² + 3n + 2 = (n + 1)(n + 2).
n2 + 3n + 2 is a product of two integers each greater than 1, and so n2 + 3n + 2 is not prime.
Rational numbers(유리수)
rational number = if and only if it can be expressed as a quotient of two integers with a anonzero demonimator. 분모가 0이 아닌 정수인 분수로 나타낼 수 있는 수
irrational number = 무리수. 유리수와 무리수는 둘다 실수에 속함. 무리수 예시) π
Is 0 a rational number?
Yes, 0 = 0 ∕ 1.
Is 2 ∕ 0 an irrational number?
No, because every irrational number is a real number, and 2 ∕ 0 is not a real number.
Is 0.12121212… a rational number?
Yes. 0.121212… = 12/99
Q) Prove that every integer is a rational number
Proof.
Suppose n is any [particular but arbitrarily chosen] integer.
Then n = n · 1, and so n = n / 1 by dividing both sides by 1.
Now n and 1 are both integers, and 1 ≠ 0.
Hence n can be written as a quotient of integers with a nonzero denominator, and so n is rational.
Corollary
Corollary = 따름 정리
이미 증명된 정리로 인해서 즉시 증명될 수 있는 statement
Theorem 4.3.2) The sum of any two rational number is rational.
Corollary) The double of a rational number is rational
Proof: Suppose r is any rational number. Then 2r = r + r is a sum of two rational numbers.
So, by Theorem 4.3.2 (the sum of any two rational numbers is rational), 2r is rational.
Divisibility(나뉨성)
If n and d are integers then n is divisible by d if, and only if, n equals d times some int and d ≠0.
n을 d의 정수곱으로 나타낼 수 있다면 n은 d로 나뉜다. n is divisible by d
= d is a factor of n, d is a divisor of n = d | n
d | n ⇒ 적어도 하나이상의 정수 k에 대해 n = dk
Is 7 a factor of −7?
Yes, −7 = 7 · (−1).
If k is any nonzero integer, does k divide 0?
Yes, because 0 = k· 0.
1의 divisor는 1과 -1뿐이다.
If a and b are integers, is 3a + 3b divisible by 3?
Yes. By the distributive law of algebra,
3a + 3b = 3(a + b) and a + b is an integer because it is a sum of two integers.
Nondivisibility
d|n ⇔ ∃ an integer k such that n = dk and d != 0
n/d가 정수가 아니면 non divisible
divisibility로 prime number를 재정의하면 positive integer divisor가 1과 자기자신밖에 없는 수
Transitivity
모든 정수 a,b,c에 대해서 a가 b를 나누고 b가 c를 나누면 a는 c를 나눌 수 있다.
By definition of divisibility, b = ar and c = bs for some integers r and s.
By substitution, c = bs = (ar)s = a(rs)
Let k = rs, then k is an integer (product of integers).
Therefore, c = ak where k is an integer
Thus a divides c by the definition of divisibility.
Unique Factorization of integers theorem
1이상의 정수 n은 prime number를 통해 나눌 수 있다.
1 이상의 어떤 정수든 prime number나 prime number의 곱으로 표현할 수 있다.
Q)Suppose m is an integer such that
8· 7· 6· 5· 4· 3· 2· m = 17· 16· 15· 14· 13· 12· 11· 10.
Does 17 | m?
A) Since 17 is one of the prime factors of the right-hand side of the equation, it is also a prime factor of the left-hand side (by the unique factorization of integers theorem).
But 17 does not equal any prime factor of 8, 7, 6, 5, 4, 3, or 2 (because it is too large).
Hence 17 must occur as one of the prime factors of m, and so 17 | m
Quotient-remainder theorem ( 몫과 나머지 정리)
모든 정수 n과 양의 정수 d에 대해 n = dq + r and 0≤ r < d 를 만족하는 정수 q와 r이 존재한다.
q = quotient, r = remainder
Div and Mod
n / d = n div d = integer quotient를 얻음
n % d n mod d = nonnegative integer remainder를 얻음
Q) Suppose today is Tuesday, and neither this year nor next year is a leap year.
What day of the week will it be 1 year from today?
365 div 7 = 52 and 365 mod 7 = 1 because 365 = 52 * 7 + 1.
따사서 수요일이다.
Method of Proof by division into cases
p ∨ q
p → r
q → r
∴ r
Q) Prove that given any two consecutive integers, one is even and the other is odd.
Case 1 (m is even): In this case, m = 2k for some integer k, and so m + 1 = 2k + 1, which is odd [by definition of odd].
Hence in this case, one of m and m + 1 is even and the other is odd.
Case 2 (m is odd): In this case, m = 2k + 1 for some integer k, and so m + 1 = (2k + 1) + 1 = 2k + 2 = 2(k + 1). But k + 1 is an integer because it is a sum of two integers.
Therefore, m + 1 equals twice some integer, and thus m + 1 is even. Hence in this case also, one of m and m + 1 is even and the other is odd.
It follows that regardless of which case actually occurs for the particular m and m + 1 that are chosen, one of m and m + 1 is even and the other is odd.
Q) Show that any integer can be written in one of the four forms
n = 4q or n = 4q + 1 or n = 4q + 2 or n = 4q + 3 for some integer q.
Given any integer n, apply the quotient-remainder theorem to n with the divisor equal to 4.
This implies that there exists an integer quotient q and a remainder r such that
n = 4q + r and 0 ≤ r < 4.
But the only nonnegative remainders r that are less than 4 are 0, 1, 2, and 3.
Hence, n = 4q or n = 4q + 1 or n = 4q + 2 or n = 4q + 3 for some integer q.
In other words, n mod 4 equals 0, 1, 2, or 3.
Absolute value
Triangle inequality
For all real numbers x and y, |x+y| ≤ |x|+|y|.
Proof: Suppose x and y are any real numbers.
Case 1 (x + y ≥ 0): In this case, | x + y | = x + y, and by lemma,
x ≤ | x | and y ≤ | y |
| x + y | = x + y ≤ | x | + | y |
Case 2 (x + y ≤ 0): In this case, | x + y | = − (x + y) = (−x) + (−y), and by lemma,
− x ≤ | −x | = | x | and − y ≤ | −y | = | y |.
| x + y | = (−x) + (−y) ≤ | x | + | y |
Hence In both cases | x + y | ≤ | x | + | y |
indirect arugment
우회적인 방법을 통한 증명 중 하나⇒ contradiction을 통한 증명
statement가 true와 false중 하나만 해당할 수 있다는 것을 이용.
Method of proof by contradiction
증명할 statement가 false라고 가정한다. (negation이 true라고 가정)
그 가정이 논리적으로 모순으로 이어짐을 보인다. 따라서 statement가 true임을 보인다.
Q)Use proof by contradiction to show that there is no greatest integer.
Proof.
Suppose not.
That is, suppose there is a greatest integer N.
Then N ≥ n for every integer n.
Let M = N + 1. Now M is an integer since it is a sum of integers.
Also M > N since M = N + 1.
Thus M is an integer that is greater than N.
So N is the greatest integer and N is not the greatest integer, which is a contradiction.
Method of proof by Contraposition
대우를 통한 증명. 증명할 statement를 contrapositive form으로 옮긴 후에 contrapositive를 direct proof를 통해서 증명한다.
Q)Prove that for every integer n, if n 2 is even then n is even
Proof.
Contrapositive: For every integer n, if n is not even then n2 is not even.
Suppose n is any odd integer. [We must show that n2 is odd.]
By definition of odd, n = 2k + 1 for some integer k. By substitution and algebra,
n2 = (2k + 1)2 = 4k2 + 4k + 1 = 2(2k2 + 2k) + 1.
Now 2k2 + 2k is an integer because products and sums of integers are integers.
So n2 = 2 * (an integer) + 1, and thus, by definition of odd, n2 is odd