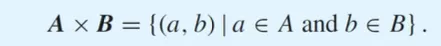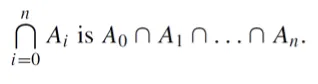Set Theory

Sets

A set is an unordered collection of objects.

It is completely determined by what its elements are – The order in which they might be listed does not matter – Some elements might be listed more than once.

집합에 포함된 object들을 elements, member라고 부른다. 집합에 포함되는 원소인지 여부를

x ∈ S and x ∉ S 로 표현한다.

Set-roster notation(원소나열법)

Examples

•

Set of all vowels in the English alphabet:

V = {a,e,i,o,u}

•

Set of all odd positive integers less than 10:

O = {1,3,5,7,9}

•

Set of all positive integers less than 100:

S = {1,2,3,……..,99}

•

Set of all integers less than 0:

S = {…., -3,-2,-1}

Is {0} = 0?

{0} ≠ 0 because {0} is a set with one element, namely 0, whereas 0 is just the symbol that represents the number zero.

How many elements are in the set {1, {1}}?

The set {1, {1}} has two elements: 1 and the set whose only element is 1.

Important Sets

N = natural numbers = {0,1,2,3….}

Z = integers = {…,-3,-2,-1,0,1,2,3,…}

Z⁺ = positive integers = {1,2,3,…..}

R = set of real numbers

R+ = set of positive real numbers

C = set of complex numbers.

Q = set of rational numbers

set-builder notation(조건제시법)

S = {x | P(x) } ⇒ predicate

Positive rational numbers: Q+ = {x ∈ R | x = p / q, for some positive integers p, q }

Interval Notation

[ a, b ] = { x | a ≤ x ≤ b }

[ a, b ) = { x | a ≤ x < b }

( a, b ] = { x | a < x ≤ b }

( a, b ) = { x | a < x < b }

Closed interval [ a, b ]

Open interval ( a, b )

Sets and Elements

집합이 집합의 원소가 될 수 있다.

공집합은 공집합을 포함한 집합과 다르다. ∅ ≠ { ∅ }

Set equality

– Two sets are equal if and only if they have the same elements.

– There fore if A and B are sets, then A and B are equal if and only if ∀x (x ∈ A x ∈ B)

– { 1, 3, 5 } = { 3, 5, 1 }

– { 1, 5, 5, 5, 3, 3, 1 } = { 1, 3, 5 }

Subsets (부분집합)

A ⊆ B

A가 B의 부분집합이다 = A의 모든 원소를 B가 가지고 있다.

(a) 2 ∈ {1, 2, 3}

(b) {2} ∈ {1, 2, 3}

(d) {2} ⊆ {1, 2, 3}

(e) {2} ⊆ {{1}, {2}}

(f) {2} ∈ {{1}, {2}}

(a), (d), and (f) are true

Empty set and Universal Set

아무 원소도 가지지 않는 집합 = 공집합 {} = Ø

empty set (or null set, 공집합) and denote it by the symbol Ø (or {}).

universal set U is the set containing everything currently under consideration

Russell’s Paradox

어떤 마을의 이발사는 다음과 같이 선언했다. “앞으로 나는‘스스로 면도하지 않는’ 모든 사람을 면도해 줄 것 이오. 다만‘스스로 면도하는’ 사람은 면도하지 않겠소.” 이 때 이 이발사는 스스로 면도할 수 있는가?

변형: 어떤 법원에 어떤 법원에 식인종이 사람을 잡아먹은 죄로 판결을 받게 되었다. 판사는"넌 사람을 죽였으니 너역시 죽음을 피할 수 없다. 죽기전에 마지막으로 한마디만 할 수 있는 시간을 줄텐데 그 말이 사실이라면 불에 타 죽을 것이며, 거짓이라면 물에 빠져 죽을 것이다." 라고 말했다. 여기서 식인종은 정말로 딱 한마디를 했다. 하지만 식인종은 죽지않고 풀려나게 되었다. 과연 식인종은 무슨 말을 하고 풀려나게 되었을까?

A) 나는 물에 빠져 죽을 것이다.

Ordered Pair (순서쌍)

(a, b) = (c, d) 이기 위해서는 a=c, b=d여야 한다.

a. Is (1, 2) = (2, 1)?

No. By definition of equality of ordered pairs, (1, 2) = (2,1) if, and only if, 1 = 2 and 2 = 1. But 1 ≠ 2, and so the ordered pairs are not equal.

Cartesian products (데카르트 곱)

A X B = A cross B = 순서쌍 (a, b)의 가능한 모든 경우의 집합. (a는 A의 원소, b는 B의 원소)

Let A = {1, 2, 3} and B = {u, v}.

a. Find A × B, B × A, and B × B

A × B = {(1, u), (2, u), (3, u), (1, v), (2, v), (3, v)}

B × A = {(u, 1), (u, 2), (u, 3), (v, 1), (v, 2), (v, 3)}

B × B = {(u, u), (u, v), (v, u), (v, v)}

세 개 이상의 Cartesian product은 두개의 데카르트 곱을 순차적으로 적용한것과 같다.

Set Equality (집합 상등)

To know that a set A equals a set B,

you must know that A ⊆ B and you must also know that B ⊆ A.

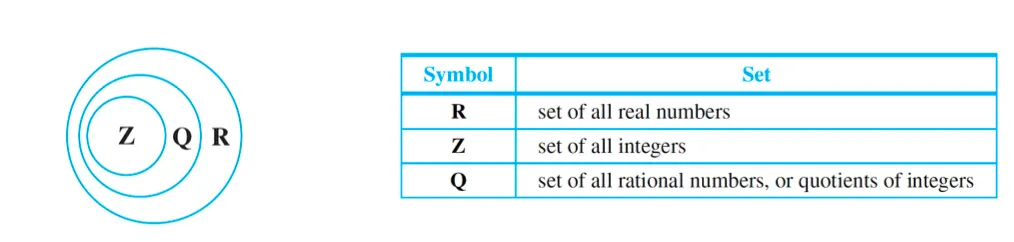
Venn Diagram

Z is a subset of Q because every integer is rational (any integer n can be written in the form 1/n)

•

Q is a subset of R because every rational number is real (any rational number can be represented as a length on the number line).

•

Z is a proper subset of Q because there are rational numbers that are not integers (e.g., 1/2).

•

Q is a proper subset of R because there are real numbers that are not rational (e.g., 2).

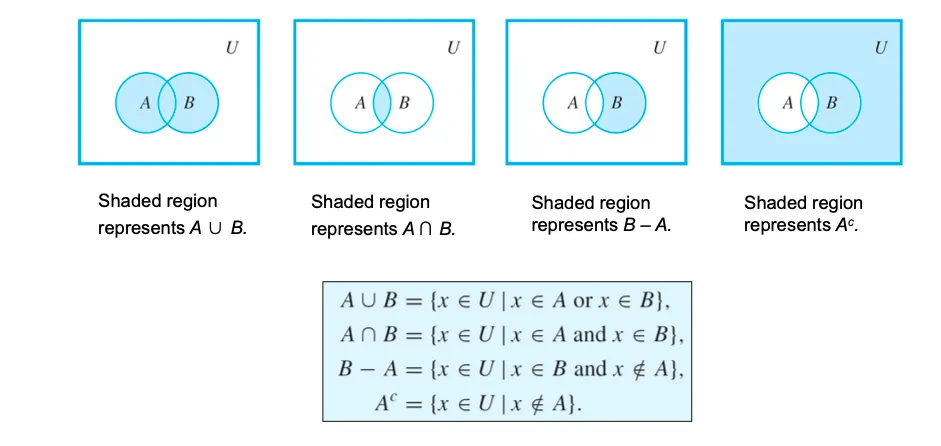
Operations on Sets

Union (합집합)

Intersection (교집합)

Difference (차집합)

Complement (여집합)

Operations on more than two Sets

Unions of IndexedCollection of sets

Intersections of IndexedCollection of sets

Disjoint sets

disjoint = 서로소

하나의 집합이 서로 겹치지 않는 서로소인 집합으로 나뉘는 것을 partition(분할)이라고 한다.

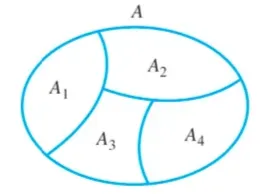
Suppose A, A1, A2, A3, and A4 are the sets of points represented by the regions shown in the figure,

•

Then A1, A2, A3, and A4 are subsets of A, and A = A1 U A2 U A3 U A4.

•

Boundaries are assigned to the regions representing A2, A3, and A4

in such a way that these sets are mutually disjoint.

Then A is called a union of mutually disjoint subsets,

and the collection of sets {A1, A2, A3, A4} is said to be a partition of A.

Power Sets (멱집합)

𝓟(A) = set of all subsets of A

Find the power set of the set {x, y}. That is, find 𝓟({x, y}).

𝓟({x, y}) is the set of all subsets of {x, y}.

We know that Ø is a subset of every set, and so Ø ∈ 𝓟({x, y}).

Also any set is a subset of itself, so {x, y} ∈ 𝓟({x, y}).

The only other subsets of {x, y} are {x} and {y}, so

𝓟({x, y}) = {Ø, {x}, {y}, {x, y}}